Ciencia & Futuro
V. 13. No. 3 septiembre-noviembre 2023
ISSN 2306-823X
Recibido: 27 febrero 2023/ Aceptado: 7 julio 2023
Diseño de un sistema de bombeo a escala experimental en la Universidad de Moa
Design of a pumping system on an experimental scale at the University of Moa
Lisander Romero Breffe lromerob@ismm.edu.cu
Michel Rodríguez Ismar mrismar@ismm.edu.cu
Alexey Coba Louzado aclouzado@ceproni.moa.minen.cu
Universidad de Moa (Cuba).
Resumen: Se realizó una proyección de una instalación a escala experimental de hidrotransporte con el objetivo de hacer pruebas hidráulicas para diferentes fluidos utilizados en las industrias. Se aplicó una metodología de cálculo en función de las características del fluido a manipular (agua cruda) con el objetivo de evaluar las pérdidas por rozamiento en el sistema de tuberías y accesorios instalado, con vista a la selección del grupo moto-bomba a emplear. Los resultados revelaron que el grupo moto-bomba de la marca SACI PUMPS bomba centrífuga KDN 32/125,1 con un punto de operación de 21 m3/h de caudal y una altura de presión de 16 m, con un rendimiento de 59 % y una potencia consumida por el motor de la bomba de 1,61 kW, para un número de revoluciones de 2 900 rev/min es idóneo para la instalación de bombeo propuesta.
Palabras clave: fluido industrial; hidrotranspotación; instalación hidráulica; red hidráulica.
Abstract: A projection of an experimental scale hydrotransport facility was carried out with the objective of carrying out hydraulic tests for different fluids used in industries. A calculation methodology was applied based on the characteristics of the fluid to be handled (raw water) with the objective of evaluating friction losses in the installed pipe and accessory system, with a view to selecting the motor-pump group to be used. The results revealed that the SACI PUMPS brand motor-pump group KDN 32/125.1 centrifugal pump with an operating point of 21 m3/h flow rate and a pressure head of 16 m, with a performance of 59 % and a power consumed by The pump motor of 1.61 kW, for a number of revolutions of 2 900 rev/min is ideal for the proposed pumping installation.
Key words: industrial fluid; hydrotranspotation; hydraulic installation; hydraulic network
En la Universidad de Moa, existen áreas e instalaciones destinadas al estudio y comportamiento de los fluidos industriales, en especial del níquel, así como los elementos y equipos que componen dichas instalaciones (Pérez, Garcell y Hernández, 2020; Rodríguez et al., 2021; Hernández-Ramírez et al., 2021).
La instalación semi-industrial de hidrotransporte construida alrededor entre 1985 y 1986, es una de estas áreas destinadas para la investigación y la docencia, la misma consta de bombas, tuberías, accesorios e instrumentación destinados al control de los parámetros de funcionamiento de estos equipos para el bombeo de diferentes fluidos. Se dispone de un sistema de redes en circuito cerrado y semi-abierto por el cual se trasiegan los fluidos en estudio (agua y pulpas principalmente).
No se cuenta con una instalación de hidrotransporte experimental de menor escala a la ya existente, que traiga consigo un menor consumo de energía y un mejor aprovechamiento de los recursos minerales como es la cantidad de material a manipular, ya que la actual existente en el departamento de Mecánica específicamente en el área de Mecánica de los Fluidos de la Universidad de Moa es a escala semiindustrial lo que provoca grandes consumos de energía y complicaciones en la manipulación del fluido.
El objetivo del trabajo es proyectar un sistema de hidrotransporte a menor escala en la estación experimental de la Universidad de Moa, que permita un mejor aprovechamiento de los materiales a manipular y disminuir los consumos energéticos.
Materiales y métodos
Para determinar el punto de operación de la bomba centrífuga y así su selección en la estación experimental en función del sistema de tuberías y accesorios perteneciente al laboratorio de hidrotransporte de la Universidad de Moa, se utiliza como fluido universal agua cruda a una temperatura ambiente de 26 0C.
Las propiedades del agua se dan a partir de la temperatura de trabajo que se va a analizar en la instalación experimental (Rodríguez, 2013; Reza, 2000; Do Nascimento & Rodríguez, 2020).
Proyección de la instalación experimental en la estación de bombeo de la Universidad de Moa
Se requiere proyectar una instalación a escala experimental de hidrotransporte en el laboratorio de hidráulica perteneciente a la Universidad de Moa, con vista a analizar el comportamiento de diferentes fluidos utilizados en la industria por tuberías y su influencia en la bomba.
Características del tanque a utilizar en la instalación experimental de hidrotransporte
El tanque está compuesto por un cilindro y un ovoide (Figura 1).
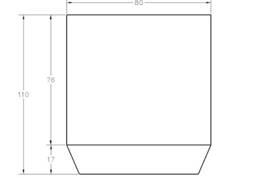
Figura 1. Tanque de la instalación experimental de la Universidad de Moa.
El cálculo del volumen del tanque se realiza por la ecuación:
Vtanque = Vcil +Vovoide
Dónde:
Vcil: Volumen del cilindro, (m3);
Vovoide: Volumen del ovoide que se determina, (m3).
El volumen del cilindro se calcula por la ecuación:
![]()
Dónde:
d: Diámetro del cilindro, (m);
h: Altura del cilindro, (m).
El cálculo del volumen del ovoide se plantea por la ecuación:
![]()
Dónde:
a: Ancho, (m);
b: Largo, (m);
c: Altura (m).
Características de los elementos constructivos de la instalación experimental de la Universidad de Moa
Se considera para la proyección de la instalación experimental tuberías de acero al carbono según la norma ANSl y los códigos B.36.10 y B.36.1, utilizando tuberías estándar (STD). La instalación a proyectar se muestra en la figura 2, donde se aprecian las longitudes de tuberías y cantidad de accesorios que contará la instalación, estas longitudes se expresan en centímetros.
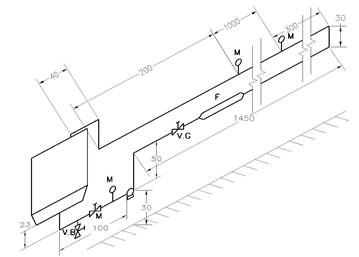
Figura 2. Proyección de la instalación a escala experimental perteneciente a la Universidad de Moa.
La misma cuenta con:
-Tanque (TK) en el que se deposita el material a transportar
-Agitador acoplado a su árbol para homogenizar la mezcla
-Moto bomba centrífuga que es la encargada de bombear el fluido de forma continua
-Moto reductor que es el que mueve el agitador.
La instalación experimental está compuesta por siete codos de 90 grados, una válvula de compuerta emplantillada clase 150 lb, con vástago elevable con rosca externa, una válvula de globo, una válvula de bola y una Te. Además, cuenta con instrumentación de medición como son toma de presión en los puntos ubicados en la succión y descarga de la bomba, también se cuenta con manómetros en un tramo de longitud recta de 10 m respectivamente para determinar las pérdidas hidráulicas. La instalación tiene un flujómetro magnético para conocer la cantidad de material que circula por la tubería. Al concluir las corridas a realizar se limpia la instalación en circuito abierto mediante la válvula de drenaje (válvula de bola).
Longitud en la succión de la bomba:
-Longitud de la tubería de succión 1,23 m
-Longitud de la tubería de impulsión de 31,6 m
Determinación del diámetro óptimo de la instalación a escala experimental de la Universidad de Moa
El cálculo de los diámetros preliminares depende de la velocidad de conducción dentro del tubo, para tal efecto se utiliza la ecuación: Q = V A
Dónde:
V![]() : Velocidad media del
fluido, (m/s);
: Velocidad media del
fluido, (m/s);
Q: Caudal transportado por la bomba, (m3/s);
A: Área de la sección transversal de la tubería, (m2).
Despejando el diámetro del cálculo del área se obtiene la expresión:
![]()
Dónde:
Di: Diámetro interior de la tubería, (m).
Despejando el diámetro interior se obtiene:
![]()
Luego de calculado el diámetro interior de la tubería, se estandariza su valor según las especificaciones técnicas para tuberías de acero al carbono según la norma ANSl y los códigos B.36.10 y B.36.1, utilizando tuberías estándar (STD).
Se corrige nuevamente el valor de la velocidad del fluido por la ecuación:
![]()
Cálculo del número de Reynolds
El número de Reynolds (Re), que permite establecer el régimen de trabajo según la naturaleza reológica del fluido se determina por la ecuación:
![]()
Dónde:
mp:
Viscosidad plástica del fluido, (Pa![]() s);
s);
ρ: Densidad del agua, (kg/m3).
Cálculo del factor de fricción
Para el cálculo del factor de fricción se determina auxiliándose por el diagrama de Moody (Reza, 2000), para tuberías rugosas según el número de Reynolds.
Cálculo de las pérdidas por rozamiento en las tuberías
En la impulsión de la bomba:
El cálculo de las pérdidas por rozamiento en la tubería de impulsión h1 (m), se calculan por la ecuación de Nekrasov (1986):
![]()
Dónde:
f: Factor de fricción;
L: Longitud de la tubería de succión, (m);
El cálculo de las pérdidas locales en la tubería de impulsión h2 se determina por:
![]()
Dónde:
xt: Sumatoria de los coeficientes de pérdidas locales para accesorios y las tuberías comerciales nuevas, de acero con flujo en la zona de total turbulencia (Reza, 2000).
La sumatoria de los coeficientes de pérdidas locales se calcula teniendo en cuenta los accesorios existentes en la línea de impulsión:
xt =2xv +6xc+xs
En la tabla 1 se muestran los valores de los coeficientes de pérdida locales para los accesorios instalados en la línea de impulsión.
Tabla 1. Coeficientes de pérdidas locales para la línea de impulsión de DN
|
Accesorios |
Cantidad |
Coeficiente de resistencia ξ |
|
Salida de la tubería al tanque |
1 |
1 |
|
Válvula de globo |
1 |
0,057 |
|
Flujómetro |
1 |
0,057 |
|
Codo de 90 |
6 |
0,57 |
Las pérdidas totales en ese tramo de tubería y accesorios se calculan:
himp=h1+h2
En la succión de la bomba:
El cálculo de las pérdidas por rozamiento en la tubería de succión se calcula por:
![]()
Dónde:
v: Velocidad de transportación del fluido, (m/s).
El cálculo de las pérdidas locales en la tubería de succión en metros de columna líquida se realiza por la ecuación de Nekrasov (1986):
![]()
Dónde:
xt: Sumatoria de los coeficientes de pérdidas locales para accesorios y las tuberías comerciales nuevas, de acero con flujo en la zona de total turbulencia (Reza, 2000).
La sumatoria de los coeficientes de pérdidas locales en la succión de la bomba se calcula por la ecuación:
xt = xc + 2xv + xtee
x: Coeficientes de pérdidas locales para las tuberías comerciales nuevas, de acero, con flujo en la zona de total turbulencia (Reza, 2000).
En la tabla 2 se muestran los valores de los coeficientes de pérdidas locales para los accesorios instalados en la succión de la bomba.
Tabla 2. Coeficientes de pérdidas locales para la línea de succión.
|
Accesorios |
Cantidad |
Coeficiente de resistencia x |
|
Te |
1 |
0,38 |
|
Válvula de compuerta |
1 |
0,152 |
|
Codo de 90 |
1 |
0,57 |
Las pérdidas totales en ese tramo de tubería y accesorios se calculan:
hsucc=h1+h2
El cálculo de las pérdidas totales dinámicas para la instalación de tuberías y accesorios, se determinan mediante la ecuación hdin=himp+hsuc
Para el cálculo de la altura estática se plantearon dos condiciones del nivel mínimo y nivel máximo, del líquido en el tanque.
El cálculo de la altura estática se realizó por la ecuación:
ΔZ = Himp - Hsuc
Para la condición del máximo nivel del líquido en el tanque se utilizaron las alturas estáticas:
Himp = 1,16
Hsucc = 1m
El cálculo de las pérdidas totales en el sistema se realizó por la ecuación
ht = hdin + ΔZ
La característica de la red del sistema de tuberías en la instalación de hidrotransporte se calcula por la ecuación de Nekrasov (1986).
![]()
Dónde:
Rc: Coeficiente generalizado de resistencia de la red exterior de la instalación de transporte hidráulico, (s2/m5);
DZ: Altura estática, (m);
Q: Caudal transportado por las bombas, (m3/s).
Para el cálculo de la resistencia de la red en tuberías y accesorios se determina:
![]()
Dónde:
L: Longitud equivalente total del sistema que incluye tuberías rectas y accesorios, (m).
Se puede determinar la longitud equivalente en metros columna líquida para los diferentes accesorios existentes en el sistema utilizando la ecuación:
![]()
Dónde:
L/Dvalglo: Longitud equivalente de la válvula de globo, m;
L/Dflu: Longitud equivalente del flujómetro, m;
L/DC: Longitud equivalente del codo, m;
L/DTe: Longitud equivalente de la te, m;
L/DVC: Longitud equivalente de la válvula de compuerta, m;
DN: Diámetro nominal, m.
Comprobación de la condición de ausencia de cavitación
Para la comprobación de la condición de ausencia de cavitación se utiliza la ecuación propuesta por Favier (2021):
NPSHd D NPSHr
Dónde:
NPSHr: Altura neta de succión requerida en la succión de la bomba, m;
NPSHd: Altura neta de succión disponible en la succión de la bomba, m.
Para la determinación de la altura neta de succión disponible se utiliza la ecuación:
![]()
Dónde:
Patm: Presión atmosférica (Pa), (Romero, 2022).
hsucc: Pérdida hidráulica por fricción en la succión de la bomba, (m).
Hs: Altura de succión para el mínimo y el máximo nivel del líquido en tanque, (m).
pv: Tensión de vapor, (m).
g: Peso específico del fluido, (N/m3).
Metodología de cálculo para el balance energético de una bomba centrífuga
El balance energético de una bomba se sustenta en el cálculo del rendimiento total y en la potencia real que consume el motor. La metodología a utilizar se establece según Nekrasov (1986).
Potencia útil que se le entrega al eje de la bomba
La potencia útil que se le entrega al eje de la bomba depende del rendimiento de la misma y se calcula por la expresión:
![]()
Dónde:
r: Densidad del fluido a transportar, (kg/m3);
H: Pérdida o carga a que está impuesta a vencer la bomba, (m);
Q: Caudal que transporta la bomba, (m3/s);
h:
Eficiencia de la bomba, (de 0![]() 1);
1);
Neje: Potencia útil que se le entrega al eje de la bomba, (kW).
Potencia real que consume el motor
La potencia que consume el motor tiene que ser mayor que la potencia suministrada por el eje de la bomba, la cual es expresada por:
Nm = (1,02+1,05) Neje
Dónde:
Nm: Potencia consumida por el motor, (kW).
El valor del coeficiente (1,05…1,1) es la reserva de energía del motor según los estándares de fabricación del mismo.
Resultados y discusión
Parámetros generales de diseño en la instalación experimental de la Universidad de Moa
En la tabla 3 se muestran los resultados obtenidos a partir de las ecuaciones. El volumen total del tanque es de 0,837 m3
Tabla 3. Resultados del volumen del tanque
|
Parámetro |
Resultado |
Unidad |
|
Volumen del tanque (Vtanque) |
0,837 |
m3 |
|
Volumen del cilindro (Vcil) |
0,381 |
m3 |
|
Volumen del ovoide (Vovoide) |
0,455 |
m3 |
Resultados de los cálculos de la instalación experimental de la Universidad de Moa
En la tabla 4 se muestran los resultados de los distintos parámetros reflejados en la metodología de cálculo, para los cuales se usó un caudal de 0,0058 m3/s.
Tabla 4. Resultado de los cálculos del diámetro óptimo de la tubería, la velocidad media y el número de Reynolds
|
Parámetro |
Resultado |
Unidad |
|
Diámetro interior (Di) |
0,054 |
m |
|
Velocidad del fluido (v) |
2,54 |
m/s |
|
Reynolds (Re) |
171 248 |
- |
|
Factor de fricción (f) |
0,015 |
- |
El diámetro óptimo calculado del sistema de tuberías y accesorios para un caudal de 21 m3/h resultó ser un valor de 0,054 m, que esto equivale a una tubería de 2 pul de diámetro nominal según las especificaciones técnicas para tuberías de acero comerciales (norma ANSI y los códigos B.36.10 y B.36.1, utilizando tuberías estándar STD). El número de Reynolds calculado para el transporte de agua cruda mostrado en la tabla demuestra un comportamiento turbulento del fluido, superando los límites establecidos en la zona de transición del régimen laminar al turbulento en los regímenes evaluados de alrededor de 4 000.
En la tabla 5 se muestra el valor del factor de fricción determinado en función del número de Reynolds y la rugosidad relativa de 0,009 para tuberías de acero comercial (Romero 2022), obtenidos por el diagrama de Moody (Reza, 2020).
Tabla 5. Resultado de los cálculos de las pérdidas por rozamiento y locales en la tubería de succión y la tubería de impulsión
|
Parámetros (m) |
Impulsión |
Succión |
|
Pérdidas por rozamiento en la tubería (h1), m |
2,88 |
0,11 |
|
Pérdidas locales en la tubería (h2), m |
1,49 |
0,41 |
|
Coeficientes de pérdidas locales para accesorios y las tuberías (xt) |
4,53 |
1,25 |
|
Pérdidas totales del sistema (himp) y (hsucc), m |
4,37 |
0,52 |
|
Pérdidas dinámicas (hdin), m |
4,90 |
|
|
Altura estática para el mínimo nivel del líquido en el tanque (ΔZ), m |
0,76 |
|
|
Altura estática para el máximo nivel del líquido en el tanque (ΔZ), m |
0,16 |
|
|
Pérdida total para el mínimo nivel del líquido en el tanque (ht), m |
5,66 |
|
|
Pérdida total para el máximo nivel del líquido en el tanque (ht), m |
5,06 |
|
|
Altura requerida por el sistema de tuberías y accesorios (Hred), m |
6,15 |
|
|
Resistencia de la red de tuberías y accesorios, (Rc),(s2/m5); |
178142,4 |
|
|
Longitud equivalente del sistema de tuberías y accesorios, (Levt), m |
65,93 |
|
Como indican los resultados en la tabla 6, las pérdidas en la instalación resultan de 5,06 metros de columna de agua líquida (mcH2O), para el máximo nivel del líquido en el tanque. Para el mínimo nivel del líquido en el tanque las pérdidas son mayores de alrededor de 5,66 (mcH2O), lo que demuestra la diferencia de altura estática a vencer por la bomba, que en este caso son insignificantes. Utilizando la ecuación que describe el comportamiento de la red de tuberías y accesorios y apoyándose de ecuaciones que describen longitudes equivalentes, se comprobaron las pérdidas totales en el sistema a instalar, resultando ser de 6,15 metros de columna líquida, resultado similar al anteriormente calculado para el mínimo y máximo nivel del líquido en el tanque.
Selección de la bomba centrífuga
En la figura 3 se muestra el catálogo de la selección de la bomba centrífuga empleada en el diseño de la instalación experimental.
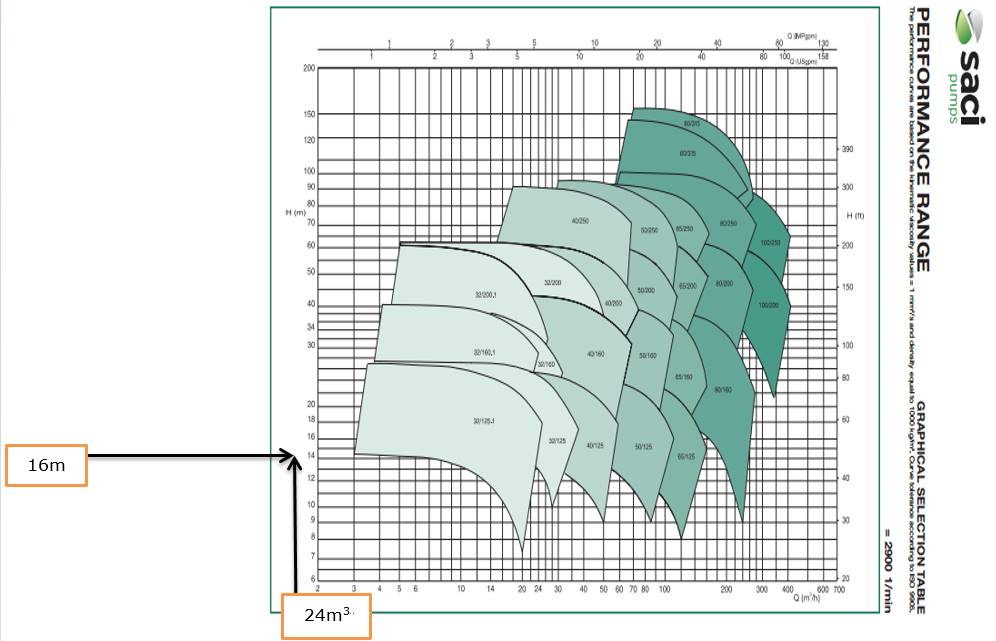
Figura 3. Selección de la bomba centrífuga en la instalación experimental.
De acuerdo a los valores calculados de altura manométrica en metros de columna líquida y el caudal del fluido a transportar, posteriormente introducidos al catálogo de la bomba a seleccionar de la marca SACI PUMPS, resultó ser la bomba centrífuga KDN 32/125,1 idónea para el sistema de bombeo evaluado, utilizando un número de revoluciones del motor de 2 900 rev/min.
La figura 4 muestra las curvas características carga−capacidad, eficiencia−capacidad de la bomba centrífuga seleccionada la cual posee una presión de trabajo de 16 metros de columna líquida (mcH2O), valor por encima del calculado para la resistencia total de la red que incluye las pérdidas dinámicas y estáticas del sistema, con una reserva de presión cercano a los 10 metros de columna líquida, para un caudal de 21 m3/h.
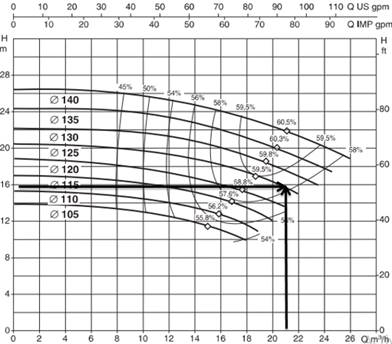
Figura 4. Selección de la carga−capacidad y eficiencia de la bomba a emplear en la instalación experimental.
Otro parámetro importante es el diámetro del impelente a utilizar de 125 mm, para un rendimiento de la bomba de 59 %.
En la figura 5 se muestran las curvas características de la altura neta de succión requerida por la bomba (NPSH)r, establecida por el fabricante de la misma.
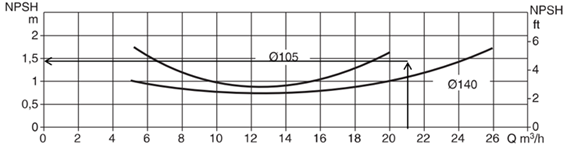
Figura 5. Curvas características del (NPSH)r y caudal para la bomba centrífuga seleccionada.
Según la figura anterior la altura neta de succión requerida por la bomba establecida por el fabricante (NPSHr) para el caudal evaluado, resultó ser de 1,45 metros de columna líquida, utilizando un diámetro de impelente de 125 mm.
En la figura 6 se muestra la potencia de la bomba que se selecciona según el caudal del fluido y el diámetro exterior del impelente.
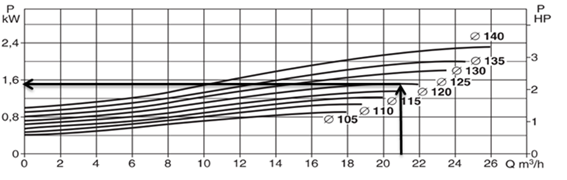
Figura 6. Curvas características de potencia y caudal para la bomba centrífuga seleccionada.
Según la figura anterior la potencia de la bomba seleccionada es de 1,5 kW resultado ser una bomba de pequeñas dimensiones y poco consumo energético.
Análisis de los resultados de los cálculos de cavitación en la bomba centrífuga seleccionada
La bomba centrífuga como cualquier otra máquina, funcionará si es adecuadamente tratada. La más importante de nuestras obligaciones es proporcionar a la bomba una altura de aspiración neta positiva, NPSH adecuado. Es decir, que el (NPSH)d debe ser igual o superior al (NPSH)r cumpliéndose la condición de ausencia de cavitación. Si está obligación no se cumple, la bomba funcionará mal en una serie de aspectos. Comenzará a cavitar, hacer ruidos y, en casos extremos sufrirá daños irreversibles (Karassik 2001; Muñoz, Velázquez & Rodríguez, 2022).
Para obtener los resultados del cálculo de cavitación se emplearon los valores del peso específico y la tensión de vapor. Otro parámetro a determinar que influye en el NPSHd es la presión atmosférica a la altura con respecto el nivel del mar. En este caso el fluido en el tanque para el diseño de la instalación experimental se encuentra alrededor de 65 metros sobre el nivel del mar, teniendo en cuenta que esta es la altura aproximada de la Universidad de Moa. Se determinó la presión atmosférica interpolando entre los valores de 0 y 200 m sobre el nivel del mar utilizando el mar (Romero, 2022), los resultados fueron de 100 500 N/m2.
Para el cálculo de la altura de succión se consideró el nivel máximo del líquido en el tanque, dando una altura de 1 metro y el mínimo nivel del líquido en el tanque de un valor 0,4 metros. Sustituyendo todos los valores calculados anteriormente en la ecuación 30, el resultado de la altura neta de succión positiva disponible (NPSH)d resultó un valor de 10,41 m de columna líquida para el máximo nivel del líquido en el tanque y para un mínimo nivel del líquido en el tanque de 9,81 m.
Estableciendo la comprobación de la condición de ausencia de cavitación que plantea que la altura neta de succión disponible debe ser mayor e igual que la altura neta de succión requerida, en este caso de 1,45 m, establecida por el fabricante, se puede demostrar la ausencia del fenómeno de la cavitación en la bomba centrífuga en estudio, para las dos condiciones de trabajo establecidas.
Resultado del balance energético de la bomba centrífuga en estudio
En la tabla 6 se muestran los valores del balance energético de la bomba seleccionada.
Tabla 6. Balance energético de la bomba
|
Parámetros |
Medidas (m) |
|
Potencia útil que se le entrega al eje de la bomba (Neje), kW |
1,53 |
|
Potencia real que consume el motor (Nm), kW |
1,61 |
Se obtienen los resultados de la potencia consumida por el eje de la bomba para un rendimiento de 59 %, siendo esta de 1,53 kW, la cual resulta inferior a la consumida por el motor a seleccionar, o sea 1,61 kW.
Conclusiones
Se proyectó un plano de la instalación de hidrotransporte a escala experimental con las dimensiones requeridas y cantidad de accesorios y equipos tecnológicos a utilizar.
Se determinaron las pérdidas totales en el sistema de tuberías y accesorios para el caudal a manipular, requiriéndose una presión de trabajo por encima de 5,66 m y 5,06 m para un mínimo y un máximo nivel del líquido en el tanque.
Se seleccionó el grupo moto-bomba a emplear, siendo de la marca SACI PUMPS bomba centrífuga KDN 32/125,1 con un punto de operación de 21 m3/h de caudal y una altura de presión de 16 m, con un rendimiento de 59 % para un número de revoluciones del motor de la bomba a 2 900 rev/min.
Referencias bibliográficas
Do Nascimento, A & Rodríguez, M. (2020). Parámetros operacionales y de diseño de la instalación semi-industrial de hidrotransporte de la Universidad de Moa. Ciencia y Futuro, 10(1), 73-86. http://revista.ismm.edu.cu/index.php/revistacyf/article/view/1896.
Favier, A. (2021). Cavitación en bombas centrífugas en el trasiego de licor producto en la planta de neutralización perteneciente a la empresa Moanickel S.A Pedro Sotto Alba. (Trabajo de Diploma). Universidad de Moa, Cuba.
Hernández-Ramírez, G., Rosa-de Armas, Y., Martínez-Rojas, R., Pelegrín-Pérez, E. & Pérez-García, L. (2021). Influencia de la concentración de sólidos en el coeficiente de corrección de carga-capacidad del transporte de hidromezclas lateríticas. Minería y Geología, 37(4), 444-457. http://revista.ismm.edu.cu/index.php/revistamg/article/view/art5_No4-2021.
Karassik, I. J., Messina, J. P., Cooper, P. & Heald, C. (2001). Pump Handbook. 3 ed. McGraw-Hill.
Muñoz, A., Velázquez, O. & Rodríguez, M. (2022). Cavitación en bombas centrífugas en el trasiego de licor producto en la planta de neutralización. Ciencia y Futuro, 12(3), 292-311. http://revista.ismm.edu.cu/index.php/revistacyf/article/view/2186.
Nekrasov, B. (1986). Hidráulica. Editorial Pueblo y Educación.
Pérez, L., Garcell, L. R. y Hernández, G. L. (2020). Modelo de viscosidad relativa que describe el comportamiento reológico de suspensiones lateríticas. Tecnología Química, 40(2), 356-375. https://tecnologiaquimica.uo.edu.cu/index.php/tq/article/view/5153.
Reza, G. (2000). Flujo de fluidos en válvulas, accesorios y tuberías. McGraw-Hill.
Rodríguez, M. (2013). Cálculo verificativo de la instalación semi-industrial de hidrotransporte del Instituto Superior Minero Metalúrgico de Moa. (Trabajo de Diploma, Instituto Minero Metalúrgico de Moa).
Rodríguez, M., Sablón, L.E., Angulo, H. & Hernández, C. (2021). Validación de nuevo modelo degradiente de presión en el hidrotransporte laminar de pulpa laterítica. Tecnología Química, 41(1), 22-33. https://tecnologiaquimica.uo.edu.cu/index.php/tq/article/download/5177/4647.
Romero, L. (2022). Propuesta de diseño de un sistema de bombeo a escala experimental en la Universidad de Moa. (Trabajo de Diploma, Universidad de Moa), Cuba.