Ciencia & Futuro
V. 14. No. 1 marzo-mayo 2024
ISSN: 2306-823X
Recibido: 7/09/2023/Aceptado: 25/01/2024
Simulación de partes y piezas de un ariete hidráulico
Simulation of parts and pieces of a hydraulic ram
Uberlandis Torrell Quinta utquinta@mecanica.ismm.edu.cu Universidad de Moa, Cuba
Eikandel Matos Mendoza emmendoza@mecanica.ismm.edu.cu Universidad de Moa, Cuba
Jesús Manuel Viera Callar jvcallar@mecanica.ismm.edu.cu Universidad de Moa, Cuba
Yaima Fernández Pérez yfperez@mecanica.ismm.edu.cu Universidad de Moa, Cuba
Rodney Martínez Rojas rmartinez@ismm.edu.cu Universidad de Moa, Cuba
Resumen: Se realizó la modelación de las partes y piezas del ariete hidráulico debido a la ausencia de los planos de diseño de un ariete ya construido y el desconocimiento de la resistencia de sus partes a las condiciones que serán sometidas. Se escogió el SolidWorks 2020 versión Premium para el diseño y simulación. Se analizaron las propiedades mecánicas de los materiales y se estableció la metodología para la modelación y simulación del ariete hidráulico. Los resultados validan el diseño del ariete hidráulico, demostrando su capacidad de resistencia. El proyecto ofrece una visión integral que abarca desde la revisión histórica hasta la validación del diseño del ariete hidráulico.
Palabras clave: bomba de agua, diseño y simulación, método de Von Mises, válvula de impulso, válvula de no retorno
Abstract: Considering there is no designing plans for an already built hydraulic ram and through the lack of knowledge about the resistance of its parts to conditions, it will be subjected, a simulation of spare parts and pieces was also carried out using SolidWorks 2020 Premium version for its design and simulation. Mechanical properties of the materials were analyzed as well as stablishing the methodology for modeling and simulation of the hydraulic ram. The results validate the design, demonstrating its resistance capacity. The project offers a comprehensive vision that ranges from the historical review to the validation of the hydraulic ram design.
Keywords: water pump, design and simulation, Von Mises method, impulse valve, non-return valve
Introducción
El ariete hidraúlico es un máquina que aprovecha la energía hidraúlica gravitatoria del agua para su elevación. El agua suministrada desciende por la tubería de carga hasta el cuerpo de la bomba para provocar una sobrepresión ocasionada por la apertura y cierre continuo de una válvula. Esta sobrepresión producida es el origen del fenómeno físico conocido como golpe de ariete y es el principio para su funcionamiento (Romero & Guerrero, 2014; Forti & Cevallos, 2022). El sistema de válvulas se hace que el agua sea impulsada a una cota mayor Usquiza, Silva & Olivares, 2022).
La simulación de partes o piezas de un mecanismo es conveniente para evaluar el rendimiento del mismo y a la vez predecir posibles fallas o roturas. Este proceder evita la pérdida de materiales y de tiempo.
Este proyecto tiene como propósito desarrollar una simulación de partes y piezas de un ariete hidráulico. Esta simulación se llevará a cabo utilizando técnicas de modelado 3D y simulación computacional a través de un software especializado. Asimismo, se realiza la modelación y simulación del comportamiento de la resistencia de las partes y piezas a partir de la presión de operación dada por un fluido, en este caso, agua.
Materiales y métodos
A partir del dimensionamiento actual del ariete y de condiciones como la presión ejercida por el fluido con un caudal determinado, se podrá obtener el comportamiento de la resistencia estructural de las partes y piezas del ariete hidráulico mediante el uso del software SolidWorks 2020 (Systemes, 2020).
Material de las partes y piezas del ariete hidráulico
La construcción del ariete hidráulico requiere el uso de materiales diversos, cada uno con propiedades mecánicas específicas. Es crucial comprender estas propiedades para simular con precisión el comportamiento del dispositivo. La resistencia, la ductilidad y la durabilidad de los materiales afectan directamente el rendimiento del ariete hidráulico. Además, la selección adecuada de materiales garantiza la seguridad y eficiencia del dispositivo, así como su vida útil. Por lo tanto, el conocimiento detallado de las propiedades mecánicas de los materiales es esencial para la construcción y el funcionamiento óptimo del ariete hidráulico (Tabla 1).
Tabla 1. Propiedades mecánicas de los materiales para la construcción del ariete
|
Campana de aire. Propiedades mecánicas del ASTM A 569 (ASTM, 2017) |
|||||||
|
Propiedades |
Módulo elástico (N/mm2) |
Coeficiente de Poisson |
Módulo cortante (N/mm2) |
Densidad de masa (kg/m3) |
Límite de tracción (N/mm2) |
Límite de compresión (N/mm2) |
Límite elástico (N/mm2) |
|
Valor |
200000 |
0,28 |
79300 |
7850 |
310 |
330 |
215 |
|
Tubería de doble T y codo de 90. Propiedades mecánicas del ASTM A 53 (ASTM, 2022) |
|||||||
|
Valor |
200000 |
0,29 |
79300 |
7850 |
330 |
300 |
205 |
|
Brida de tubería doble T y brida de codo de 90. Propiedades mecánicas del ASTM A 105 (ASTM, 2020) |
|||||||
|
Valor |
200000 |
0,28 |
85500 |
7850 |
485 |
458 |
250 |
|
Base de válvula de impulso, Acople de buje de válvula de impulso y la válvula de no retorno. Propiedades mecánicas del ASTM A 36 (ASTM, 2019) |
|||||||
|
Valor |
200000 |
0,26 |
79300 |
7850 |
400 |
- |
250 |
|
Válvula o Pistón. Propiedades mecánicas del AISI 316 (Europer, 2022) |
|||||||
|
Valor |
193000 |
0,3 |
77000 |
8000 |
550 |
650 |
205 |
|
Buje. Propiedades mecánicas del bronce al estaño |
|||||||
|
Valor |
110000 |
0,33 |
37000 |
8300 |
261,955 |
- |
110.297 |
|
Tornillos, tuercas y chicle. Propiedades mecánicas del AISI 1010 |
|||||||
|
Valor |
200000 |
0,29 |
80000 |
7870 |
325 |
- |
180 |
|
Juntas de caucho. Propiedades mecánicas del caucho NBR |
|||||||
|
Valor |
9 |
0,45 |
6 |
1150 |
15 |
12 |
7 |
Software a utilizar en el modelado y la simulación de las partes del ariete
El Software a utilizar en el modelado y la simulación de las partes del ariete es el SolidWorks 2020 versión Premium en el cual se empleará para crear modelos en 3D, realizar simulaciones y generar planos de fabricación del ariete hidráulico (Systemes, 2020).
Procedimiento para realizar el modelado
Para llevar a cabo el modelado de las piezas del ariete, que en este caso ya ha sido construido, es necesario tomar todas las medidas de las piezas físicas para utilizar SolidWorks 2020 en el modelado, garantizando así que las piezas modeladas sean una réplica exacta del original.
Procedimiento para realizar la simulación
Para poder simular se debe establecer la presión inicial, a partir de la columna de agua dada por la ecuación
P= h · g · p (pa)
Donde:
P: presión inicial, (Pa).
h: altura, ( m).
g: gravedad, (m/s2).
p: densidad ( kg/m3)
Según Arapa (2016) la eficiencia mínima de una bomba de ariete está en un 33% de la columna de agua generada por la caída del reservorio.
De acuerdo con lo anterior, la presión dentro de la bomba de ariete y por ende la de todos los elementos es la ecuación de Calderón (2021).
Pbomba= P · 1,33 (Pa)
Estos valores serán empleados para realizar las simulaciones de la válvula de impulso y de no retorno ya que en las fases se maneja la misma presión y el mismo diámetro de tubería (Calderón, 2021).
SolidWorks Simulation
Para realizar la simulación en SolidWorks se deben seguir los siguientes pasos:
- Preparación del modelo.
- Configuración de la simulación
- Definición de las restricciones y cargas
- Configuración de la malla (meshing)
- Análisis y resultados
- Interpretación de los resultados
Nota: estos son solo los pasos generales para realizar una simulación en SolidWorks Simulation. La configuración y los detalles específicos pueden variar según el tipo de análisis y las características del modelo. Es importante contar con conocimientos adecuados sobre el uso del software y las técnicas de simulación para obtener resultados precisos y confiables.
Resultados y discusión
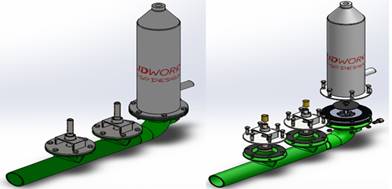
Figura 1. Ensamble del ariete hidráulico.
Con el resultado de la ecuación para determinar la Presión inicial donde h =1 m, p =1000 m3/kg y g= 9,81 m/s2 obteniendo como resultado P= 9810 Pa, con este resultado se parte a emplear la ecuación para presión en el cuerpo de la bomba de ariete en el que se obtiene un resultado Pbomba = 13047,3 Pa. A partir de este resultado se efectúa la simulación de las partes del ariete hidráulico.
Mallado y condiciones de fronteras
El mallado y las condiciones de frontera se pueden observar en las figuras (2, 3 y 4), donde el nivel de la malla varía debido a la complejidad geométrica del elemento. Esto puede apreciarse en un recuadro que expresa la distancia de cada cuadro de la malla. Además, las flechas verdes indican las zonas fijas, mientras que las flechas rojas representan la dirección y la fuerza o presión ejercida.
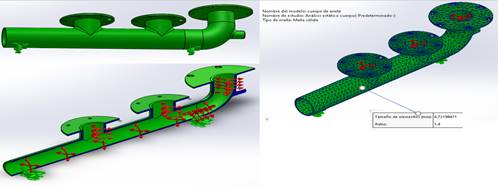
Figura 2. Mallado y condiciones de frontera en el cuerpo del ariete.
Nota: El tamaño de elementos (mm): 6,721 944 71. Las flechas verdes indican las zonas fijas y las flechas rojas el sentido de la fuerza o presión ejercida.

Figura 3. Mallado y condiciones de frontera en la válvula de impulso.
Nota: El tamaño de elementos (mm): 3,024 773 93. Las flechas verdes indican las zonas fijas y las flechas rojas el sentido de la fuerza o presión ejercida.

Figura 4. Mallado y condiciones de frontera en la válvula de no retorno.
Nota: El tamaño de elemento 1 (mm): 2,173 062 8; elemento 2 y 3 (mm): 2,716 282 86. Las flechas verdes indican las zonas fijas y las flechas rojas el sentido de la fuerza o presión ejercida.
Para la realización de la simulación de tensión máxima, el método utilizado es el de Von Mises o la máxima energía de distorsión, es cual es un criterio de resistencia estática, aplicado a materiales dúctiles.
Cuerpo del ariete
La tensión máxima en el cuerpo del ariete se representa en la figura 5.

Figura 5. Tensión máxima en el cuerpo del ariete hidráulico.
Válvula de impulso
La tensión máxima en la válvula de impulso se representa en la figura 6.
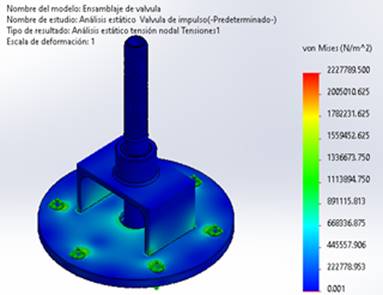
Figura 6. Tensión máxima en la válvula de impulso.
La presión generada en la bomba que se aplica a la válvula de impulso, se observa en la figura 6, la tensión máxima de 2 227 789,5 N/m^2, la cual se concentra en la geometría de la base de la válvula, como indican los colores verde y amarillo designados para los tornillos de sujeción. Este hallazgo resalta la región donde existe una mayor tensión. Por consiguiente, se concluye que la válvula no presenta riesgo de cizallamiento debido a que la tensión se concentra donde se ubican los tornillos y no en el área de trabajo de la válvula o pistón, lo que permite su operación en condiciones normales. Este resultado confirma y valida la viabilidad operativa de la válvula.
Válvula de no retorno
La tensión máxima en la válvula de impulso se representa en la figura 7.
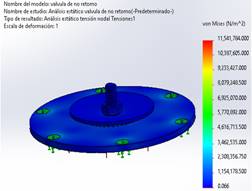
Figura 7. Tensión máxima en la válvula de no retorno.
La tensión máxima generado bajo esta presión de la bomba sobre la válvula es de 11 541 784 N/m^2, la cual se concentra en la geometría de la base de la válvula, como indican los colores verde y amarillo designados para los tornillos de sujeción donde existe una mayor tensión. Por consiguiente, se concluye que la válvula no presenta riesgo de cizallamiento debido a que la tensión se concentra donde se ubican los tornillos y no en el área de trabajo, lo que permite su operación en condiciones normales. Este resultado confirma y valida la viabilidad operativa de la válvula.
El análisis de desplazamiento mediante el método de Von Mises, indica el estiramiento que posee el material al someterlo a una carga, lo que indica si se puede cizallar o no en su funcionamiento, este valor máximo permitido debe ser menor a 1 mm.
Cuerpo del ariete
En la figura 8 se indica el desplazamiento que sufre el cuerpo del ariete al aplicarle máximas cargas.

Figura 8. Análisis de desplazamiento del cuerpo del ariete.
Todas las estructuras o componentes se deforman, al ser cargadas, y el cambio de configuración geométrica hace que sus puntos experimenten pequeños desplazamientos, como se observa en la figura 8; los colores rojos corresponden a los valores máximos de desplazamiento y los que se acercan a la gama de color azul son los mínimos; de acuerdo a esto el desplazamiento máximo que puede sufrir el material del cuerpo del ariete en condiciones de operación extremas es de 0,001 453mm, sin embargo este resultado no pone en riesgo la operatividad del cuerpo.
Válvula de impulso
El comportamiento del ariete hidráulico cuando se somete a una carga máxima permite evaluar su rendimiento y garantizar su correcto funcionamiento y seguridad. En la figura 9 se puede analizar el desplazamiento de la válvula de impulso, lo cual proporciona información sobre la respuesta del ariete hidráulico.

Figura 9. Análisis de desplazamiento de válvula de impulso.
El desplazamiento máximo sobre el material del elemento es de 0,011 mm, este desplazamiento máximo de puede observar mediante el color rojo. Sin embargo, no representa riesgo de cizallamiento o fractura del material para su funcionamiento.
Válvula de no retorno
En la figura 10 se indica el desplazamiento que sufre la válvula de no retorno, al aplicarle máximas cargas.
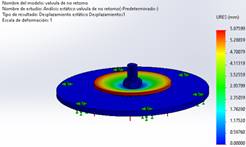
Figura 10. Análisis de desplazamiento de la válvula de no retorno.
El desplazamiento máximo es de 5,88 mm, este se puede observar mediante el color rojo en la junta de caucho NBR, en esta debe ocurrir un desplazamiento para que pueda fluir el fluido; sin embargo se observa que en la base de la válvula de no retorno se encuentra de color azul, su valor máximo de desplazamiento es de 0,588 mm aquí debe ser menor de 1 mm, por lo que no representa riesgo de cizallamiento o fractura del material para su funcionamiento.
Análisis del factor de seguridad
El factor de seguridad según el método de Von Mises debe ser superior a 1 para que el diseño de la parte o pieza sea aceptable y confiable en cuanto a la tensión o fuerza máxima, es decir que al calcular este valor debe estar por encima de este parámetro para establecer que el componente analizado cumple con las condiciones de cargas a las que se somete sin presentar deformación que afecte el funcionamiento del mismo.
En las condiciones máximas sometidas al cuerpo del ariete el factor de seguridad es 3, por lo cual se cumple la condición de ser mayor que 1 donde el elemento soportará las condiciones a las que será sometido es decir que no ofrece riesgos de deformación y cizallamiento (figura 11).
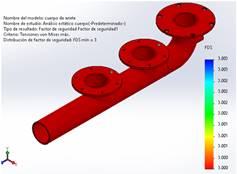
Figura 11. Análisis del Factor de seguridad en el cuerpo del ariete.
Válvula de impulso
En las condiciones máximas sometidas en la válvula de impulso el factor de seguridad es 1,1e+02 =112,219, por lo cual se cumple la condición de ser mayor que 1 donde el elemento soportará las condiciones a las que será sometido es decir que no ofrece riesgos de deformación y cizallamiento (figura 12).

Figura 12. Análisis del Factor de seguridad en la válvula de impulso.
Válvula de no retorno
En las condiciones máximas sometidas en la válvula de impulso el factor de seguridad es 22, por lo cual se cumple la condición de ser mayor que 1 donde el elemento soportará las condiciones a las que será sometido (Figura 13).

Figura 13. Análisis del factor de seguridad en la válvula de no retorno.
Aprobación de diseño del ariete hidráulico
Con el análisis exhaustivo de los resultados de las simulaciones de las diferentes partes del ariete hidráulico (cuerpo del ariete, válvula de impulso y válvula de no retorno), se evidencia que cada una de ellas es capaz de soportar la condición de 1 m de altura con una presión dentro de la bomba de 13047,3 Pa a la que serán sometida, tomando en consideración las tensiones, desplazamientos y el factor de seguridad. En base a lo anterior, el diseño del ariete ha sido aprobado al cumplir con los requisitos de resistencia, otorgando validez al ariete hidráulico ya construido.
Conclusiones
El diseño del ariete hidráulico se valida con éxito mediante simulaciones, con tensiones máximas dentro de los límites, desplazamientos menores a 1 mm en cada pieza y un factor de seguridad mayor a 1 en todos los casos.
Se confirma que el diseño cumple las condiciones de resistencia requeridas, a partir del análisis de los resultados de las simulaciones.
American Society for Testing and Materials. (ASTEM). (2017). ASTM A 569. Standard Specification foe Steel, carbón (O.15 Maximun, Percent), Hot-Rolled Sheet and strip Commercial Quality. https://www.astm.org/a0569_a0569m-91ar93e01.html.
American Society for Testing and Materials. (ASTEM). (2019). ASTM A 36. Especificación estándar para acero estructural al carbono. https://www.astm.org/a0036_a0036m-19.html.
American Society for Testing and Materials. (ASTEM). (2020). ASTM A 105 Propiedades (Mecánicas, Químicas y Clasificación). Gelson Luz blog Materiales. https://www.materiales.gelsonluz.com/2020/09/astm-a105-propiedades-mecanicas.html
American Society for Testing and Materials (ASTEM). (2022). ASTM A 53 Propiedades (Mecánicas, Químicas y Clasificación). https://www.astm.org/a0053_a0053m-22-html.
Arapa, J.B. (2016). Evaluación del rendimiento del ariete hidráulico bah-1.1/2 variando la longitud de la tubería de alimentación y condiciones de operación de la válvula de impulso. Anales científicos, 77(2), 155-165. https://revistas.lamolina.edu.pe/index.php/acu/article/view/485/pdf_23.
Calderón, E, (2021). Diseño y simulación de un prototipo de bomba de ariete para el suministro de agua en la finca El Manantial del municipio de Neiva. (Trabajo de diploma, Universidad Antonio Nariño) Colombia. http://repositorio.uan.edu.co/handle/123456789/47475.
Europer. (2022). Ficha Técnica del Acero INOX.316-316L. https://europer.cl/wp-content/uploads/2022/04/FICHAS-TECNICA-ACERO-INOX.316-316L.pdf.
Forti, B.M. & Cevallos, C.V. (2022). Sistema de bombeo para riego mediante ariete hidráulico en sectores aislados de la provincia de Manabí. Sapienza: International Journal of Interdisciplinary Studies, 3(7), 71-81. https://doi.org/10.51798/sijis.v3i7.511.
Romero, J.M. & Gutierrez, L.L. (2014). El ariete hidráulico. Proyecto e instalación en Ntongui (Angola). Diseño y Tecnología para el Desarrollo, 1, 224-237. http://polired.upm.es/index.php/distecd/article/view/2512.
Systemes, D. (2020). SOLIDWORS 2020. Dassault Systemes, San Diego.
Usquiza, B. Silva, M. Olivares, S. (2022). Rendimiento de una bomba hidráulica prototipo a diferente diámetro de tubería y singularidades. Revista de Investigación Científica UNTRM: Ciencias Naturales e Ingeniería, 5(1), 37-41. http://dx.doi.org/10.25127/ucni.v5i1.887.