Ciencia & Futuro
V. 14. No. 1 marzo-mayo 2024
ISSN: 2306-823X
Recibido: 1/09/2023/Aceptado: 7/01/2024
Determinación de las tensiones por elementos finitos de un tornillo de acero microaleado AISI 4140
Determination of stress by finite elements of an AISI 4140 micro alloyed steel screw
Roxana Pupo Matos rpmatos@minas.ismm.edu.cu Universidad de Moa, Cuba
Felix Reinier Muñoz Dranguet fmunoz@mecanica.ismm.edu.cu Universidad de Moa, Cuba
Andier Samiñón Durán andiersd@ismm.edu.cu Universidad de Moa, Cuba.
Elís Efraín Guzmán Romero eefrain@ismm.edu.cu Universidad de Moa, Cuba
Resumen: Se determinó el comportamiento a la fatiga en un tornillo de acero micro aleado AISI 4140 empleado en la culata del motor de combustión interna MAN B&W a través del Método de los Elementos Finitos. A partir de tamaño crítico de grietas de 4,2; 6,2; 8,1 y 21,6 se estableció la metodología de cálculo donde se consideró la carga distribuida de contacto y de rozamiento, las solicitaciones, el esfuerzo normal y el de corte, para determinar el fenómeno de la fractura en el tornillo. Se comprobó que la falla por fatiga del tornillo inicia con tensiones de Von Misses mínimas de 401,8 MPa; las cuales se incrementan hasta un valor máximo de 1 796 MPa; provocando la falla por fractura en los primeros filetes de rosca. La carga aplicada de 2 369 149,4 N; genera un esfuerzo cortante máximo de 104,55 Nm2, siendo este el pico máximo de resistencia antes que se produzca el fallo por fractura y que al ejercer una fuerza de 297 918,52 N; inicia un cambio en el límite elástico de este acero con la propagación de grietas, siendo el valor de 6,2 mm, la zona de transición entre las deformaciones elásticas y plásticas con incremento de la deformación.
Palabras clave: aleación, falla mecánica, fractura por fatiga, perno de sujeción
Abstract: The fatigue performance of an AISI 4140 micro-alloyed steel screw used in the cylinder head of the MAN B&W internal combustion engine was determined through the Finite Element Method. The calculation methodology was established from critical crack size of 4.2; 6.2; 8.1 and 21.6, where the distributed load of contact and friction were determined as well as the stresses, the normal and shear stress were also considered, to determine the phenomenon of fracture in the screw. It was determined that the fatigue failure of the screw begins with minimum Von Misses stresses of 401.8 MPa; which increases to a maximum value of 1,796 MPa; causing failure due to fracture in the first threads. The load of 2,369,149.4 N applied, generates a maximum shear stress of 104.55 Nm2, this being the maximum peak of resistance before failure due to fracture occurs and that when exerting a force of 297 918.52 N, initiates a change in the elastic limit of this steel with crack propagation. Therefore, the value of 6.2 mm is the transition zone between elastic and plastic deformations with an increase in deformation.
Key words: alloy, mechanical failure, fatigue fracture, clamping bolt
Introducción
Uno de los fenómenos que ocurre en las piezas que están sometidas a tensiones que varían cíclicamente con el tiempo, lo constituye la fatiga, la cual se pone de manifiesto cuando un material sometido a la acción de tensiones variables y repetidas por un período de tiempo prolongado, puede romperse bruscamente, sin deformación previa que lo muestre, bajo cargas que, si actuaran de forma estática, serían soportadas indefinidamente por el material (Budynas, 2008).
El concepto de resistencia está relacionado no solo con los efectos inmediatos de la carga, sino con la acción del tiempo. No basta que un material sea capaz de soportar la acción instantánea de la tensión máxima, sino que es preciso que sea capaz de soportar esta acción indefinidamente. Al tratar de explicarse este fenómeno en un inicio se formularon diferentes teorías.
La falla se inicia en un punto que constituye un núcleo de la misma, en el que surge una grieta y a partir de la cual la fractura va desarrollándose por fisuración progresiva, hasta que el material, cuya sección resistente va reduciéndose, no pueda soportar la tensión total que se haya sometido y se rompe bruscamente. Del examen microscópico de las fracturas por fatiga se demuestra que el inicio de la fisura se encuentra situado junto a defectos internos: estrías superficiales, cambios bruscos de sección, en puntos donde puedan existir concentraciones de tensiones (Hudgins & James, 2014).
Bajo condiciones de cargas estáticas, este hecho conduce a una cierta redistribución de las tensiones y no tiene mayor trascendencia; sin embargo, bajo cargas variables esta redistribución no se produce y los picos de tensión originan bandas de deslizamiento en los cristales, que al principio se desarrollan con mucha rapidez y luego más lentamente; estos deslizamientos plásticos, debido a que el material se está cargando y descargando continuamente, provocan un incremento local del límite elástico a consecuencia del endurecimiento del material por deformación.
En este trabajo de propone determinar el comportamiento a la fatiga en un tornillo de acero micro aleado AISI 4140 empleado en la culata del motor de combustión interna MAN B&W a través del Método de los Elementos Finitos.
Materiales y métodos
Caracterización del acero AISI 1040
En la tabla 1 se muestra la composición química estándar del acero AISI 4140, según la Alloy Casting Institute (ACI), y la designación adoptada por la AISI-SAE, de la American Society for testing Materials (ASTM).
Tabla 1. Composición química del acero AISI 4140; % en masa
|
Grado |
C |
Mn |
P |
S |
Si |
|
AISI 4140 |
0,38-0,43 |
0,75-1 |
< 0,035 |
< 0,04 |
0,15-0,35 |
|
Ni |
Cr |
Mo |
Fe |
|
|
|
< 0,25 |
0,8-1,1 |
0,15-0,25 |
Balance |
|
Propiedades mecánicas del acero AISI 4140
En la fabricación de elementos de máquinas las aplicaciones no requieren el mismo tipo de solicitaciones, ni todos los materiales responden de la misma manera, existen piezas que actúan como fusibles, donde debe evitarse la rotura de las mismas, también hay que considerar otros tipos de fallos, como una deformación excesiva (elástica o plástica) o el deterioro superficial (picado, desgaste, perdida de las propiedades deslizantes). El acero AISI 4140 presenta diferentes valores de estas propiedades en función de la temperatura de revenido. En la tabla 2 se muestran las mismas.
Tabla 2. Propiedades mecánicas del acero AISI 4140 en función de la temperatura de revenido. (Pero-Sanz y González, 2002)
|
Temperatura (oC) |
Esfuerzo último (GPa) |
σY (MPa) |
σU (MPa) |
Dureza (HRC) |
Tamaño crítico de grieta, ac mm |
|
200 |
1,93 |
297,74 |
631,99 |
56 |
4,2 |
|
300 |
1,79 |
311,28 |
631,46 |
53 |
6,2 |
|
400 |
1,59 |
289,95 |
645,68 |
48,5 |
8,1 |
|
500 |
1,23-1,33 |
270,21 |
663,29 |
38 |
21,6 |
|
600 |
0,97-1,33 |
305,53 |
636,29 |
30 |
|
|
Módulo de elasticidad (GPa) |
Tensión de rotura (MPa) |
Módulo Poissons |
|||
|
205 |
813 |
0,29 |
|||
El acero AISI 4140 presenta propiedades mecánicas en el rango desde moderadas tensiones de fluencia de 300 MPa, hasta tensiones de fluencia que superan los 1 400 MPa. Esta amplia variedad en las propiedades se logra en dependencia de la composición química y de la microestructura presente, que a su vez depende de los tratamientos térmicos que se le pueda realizar. Las mismas indican la capacidad resistente del material y constituye una referencia de cálculo para materiales frágiles, que no presentan un límite elástico diferenciado (Pero-Sanz y González, 2002).
Caracterización del espárrago roscado
Según Gainza-Legrá (2016) los grupos fuel oíl están constituidos por un motor de combustión interna, un generador sincrónico trifásico y un transformador de potencia, además de una serie de dispositivos que son los encargados del suministro de las materias primas necesarias en el proceso de combustión y generación de electricidad, así como una serie de equipos secundarios necesarios para el funcionamiento eficiente del equipamiento y la distribución de la energía.
La culata de un motor es la cubierta que cierra la parte superior de los cilindros; los pernos de sujeción (figura 1) son los elementos encargados de ejercer la fuerza necesaria para que la misma selle a los cilindros y evite el escape de los gases de combustión, así como pérdidas de presión. Al estar sujeto a vibraciones y cargas de tensión, un perno fallo en el hilo roscado, fracturándose en dos partes (Irwin, 1997).

Figura 1. Vista superior.
El elemento analizado pertenece a la culata del motor MAN B&W, cierra los cilindros por su parte superior y se une al bloque mediante tornillo. La culata está compuesta por ocho espárragos, roscado en su inferior al bloque. En la parte superior ejerce la fuerza de sujeción en la culata con una tuerca. Los espigos roscados son montados al bloque de tal forma que cada uno quede precargado con aproximadamente la misma presión de ajuste, de esta manera se garantiza que la carga de la culata sobre el bloque sea uniforme.

Figura 2. Disposición de los tornillos en el motor.
La mayoría de fallas por fractura de elementos de máquinas son fallas por fatiga; por lo general tiene lugar por una progresiva generación y crecimiento de grietas hasta obtenerse una condición crítica de fractura súbita de la sección residual resistente. Frecuentemente se observan marcas de playa, las cuales son evidencias de la posición del frente de grietas antes que se alcance la condición de fractura súbita final (Arroyo, & Álvarez, 2017).
Modelo para el análisis tenso deformacional del tornillo
Se realizó el análisis tenso deformacional originado en un tornillo, como consecuencia de la unión tornillo-tuerca. Para materiales que presentan un comportamiento elástico lineal, la relación esfuerzo deformación viene definida por la ley de Hooke. En el caso particular de trabajar con materiales isótropos, las constantes elásticas que caracterizan su comportamiento mecánico son; el módulo de Young o módulo de elasticidad (E) y el módulo de Poisson (v) (Bickford, 2007).
La geometría analizada consiste en un tornillo ISO M 56 con una fisura en superficie, sometido a diferentes condiciones de carga. Las dimensiones del tornillo son:
- Diámetro máximo: 56 mm
- Diámetro mínimo: 53,4 mm
- Radio de fondo: 52,4 mm
- Paso de la rosca: 4 mm
- Número de roscas: 35
- Longitud del tornillo: 1 866 mm
Para la representación de los esfuerzos que ejerce la tuerca al enroscarse sobre el tornillo, se consideraron las siguientes cargas, en la unión de ambos elementos:
- Carga distribuida de contacto: esfuerzo generado al enroscarse la tuerca en el tornillo.
- Carga distribuida de rozamiento: esfuerzo en contra del movimiento de enroscado de la tuerca
Para obtener el valor de la fuerza tangencial distribuida en el área total de la rosca, se considera la ecuación, que relaciona el momento exterior aplicado y la fuerza tangencial:
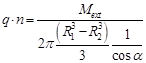
Donde:
Q: fuerza tangencial; N/m2
n: número de roscas;
Mext: momento exterior en la base del tornillo; N/m
R1: Radio exterior de la rosca, m
R2: Radio interior de la rosca, mm
Para calcular el momento torsor (Mtor) en una rosca, se ha tenido en cuenta el momento torsor sobre un anillo circular. El momento se calcula como:
Mtor = Fza · distancia
Al plantear la ecuación de continuidad para coordenadas cilíndricas quedaría de la forma, como se muestra en la ecuación:
![]()
La fuerza distribuida actúa sobre el área de la rosca, se define como:
Fza = Fza distribuida · Área
Determinación de la falla en el tornillo
El factor de intensidad de esfuerzos, para la modelación del momento tenso deformacional del tornillo se determinó según Irwin (1997):
La presencia del desgarramiento en los filetes de la rosca del agujero, sugiere que fue superada la resistencia al corte de los mismos. Para verificar lo anterior se procedió a realizar un cálculo aproximado. La carga producida por el apriete sobre el tornillo y por lo tanto sobre el agujero, estará dada según Kulak (1994) por:
![]()
Donde:
Ptor: carga aplicada sobre el tornillo; N
T: torque aplicado según plano de la autoparte, Nm
Dp: diámetro de paso; mm.
d: diámetro exterior; mm
α: ángulo de cara de rosca; grado
L: avance; mm
μ: coeficiente de fricción
El esfuerzo cortante que soportaron los filetes:
![]()
Modelado de las tensiones por elementos finitos
El modelo FEM propuesto se define automáticamente a partir de un fichero de trabajo programado en lenguaje PCL (PATRAN COMMAND LANGUAGE), sujeto a comandos especiales de MSC. El modelo FEM resultante de la ejecución de este fichero contiene las características principales siguientes:
1. Modelización geométrica y parametrizada, que permite definir la disposición matricial de tornillos, métricas y dimensiones principales de las placas como el usuario decida.
2. Mallado automático de los tornillos. Para los tornillos, elementos viga según formulación EULER-BERNOUILLI.
3. Definición automática de los casos de carga y de todos los parámetros de cálculo necesarios para la generación del fichero de entrada al programa de cálculo.
El fichero de texto generado es ejecutado por el usuario en el solver de elementos finitos utilizado, en este caso, MSC.NASTRAN. Finalmente, los resultados se importan en el post-procesador, de manera que puede realizarse un tratamiento detallado de todos los datos que se consideren interesantes (tensiones en tornillos, deformaciones del sistema, separaciones puntuales de contactos (Bursi & Jaspar, 1997).
La presente metodología, considera los modos de trabajo, la interface gráfica del usuario y el modo por bloques de programación ordenados. En la figura 3 se muestra la interfaz gráfica del usuario.

Figura 3. Interface del usuario.
Al ejecutar el software, se cierra la ventana que tiene por título Welcome to ANSYS Workbench y se selecciona el análisis a realizar, se escoge el que se muestra resaltado en color rojo, que es un análisis estático (Static Structural). En el toolbox identificado se hará doble clic y se visualiza lo que se muestra en la pantalla de la figura 4.
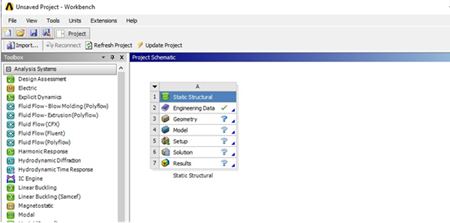
Figura 4. Selección del tipo de análisis.
Al obtener el fichero de análisis estructural, el mismo se ejecutará mediante un análisis de equilibrio “estático” en los que se leen las tensiones nodales de cada paso de tiempo, generadas por la corrida y se aplican como cargas nodales en la corrida estructural. De esta manera cada análisis estructural estático parte del estado final de deformaciones y tensiones del análisis previamente concluido. Esto es posible debido a que fue establecido que las deformaciones plásticas son “deformaciones irreversibles independientes del tiempo (si se desprecia la deformación viscoplástica a alta temperatura), de forma que entonces en dicho análisis no es necesario efectuar una integración en el tiempo.
Este análisis se realizó fundamentalmente en modo de programación.
1. Se declaró como tipo de análisis el “estático”.
2. Se empleó el método iterativo de solución de ecuaciones no lineales “FULL NEWTON RAPHSON”, que constituye el método no lineal estándar de ANSYS para problemas de plasticidad.
Para la simulación de las tensiones del acero AISI 4140 se requiere de la ejecución de la geometría para importar el modelo y definir las condiciones de frontera, con doble clic sobre Geometry, en el menú se obtienen los planos en los ejes x, y; z. En el menú File> Import External Goemetry File se ejecuta clic. En la figura 5 a se muestra el resultado que se obtiene.
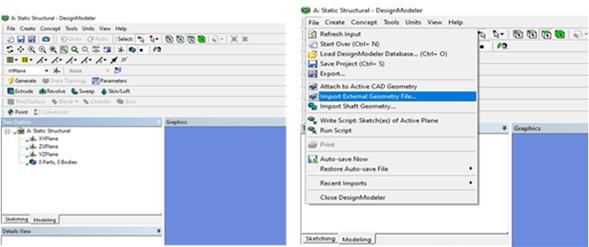
Figura 5. Obtención de los planos.
Se diseñó una geometría representativita del modelo experimental. Al seleccionar la misma, los diversos coeficientes del modelo son calculados automáticamente por el ordenador a partir de la geometría y propiedades físicas de cada elemento. A través de este procedimiento, el método se basa en dividir el modelo a validar en múltiples partes de pequeño tamaño. La división del modelo 3D en pequeñas partes divide un problema complejo en muchos problemas de mayor simplicidad que se pueden resolver de forma simultánea en menos tiempo. Los elementos comparten entre sí puntos comunes de intersección llamados nodos. Al hacer doble clic, se abre una ventana (Figura 6), la cual permite la exportación del archivo desde la ubicación donde se ha guardado el mismo, de donde se selecciona el modelo.

Figura 6. Proceso de exportación del archivo.
Para poder cargar el archivo debe de estar guardado con cualquiera de estas extensiones: *.igs, *.sat, *.dwg, *.dfx. Luego de seleccionado el archivo se presiona clic en Generate (área en rojo), y se generará el modelo seleccionado.
En el proceso de simulación, tras haber definido los materiales y sus propiedades y haber generado la geometría, se procede a construir la malla con el tipo de elemento elegido asociada a esa geometría. Para ello se debe especificar previamente el tamaño medio del elemento, que podrá reducirse posteriormente. Se ejecuta un clic derecho sobre la palabra mesh>>Generate Mesh, obteniéndose el modelo mallado mostrado en la figura 7.

Figura 7. Generación y mallado del modelo.
Debido a que los esfuerzos y deformaciones van a presentar mayores cambios en las roscas, resulta muy útil utilizar una malla fina únicamente cerca de las zonas roscadas. Al estar empleando el método-h de resolución, en la malla van a poder coexistir diferentes tamaños de elemento, con lo que se logra exactitud y resolución con ajuste de los costos computacionales adicionales. Así, las áreas del acero AISI 4140 contarán con una malla relativamente gruesa que será refinada cerca del roscado, donde los elementos de mallado serán mucho menores.
Mallado el modelo se procede a establecer las condiciones de frontera, ejecutando el comando Supports>>Fix Supports como se muestra en la figura 8.
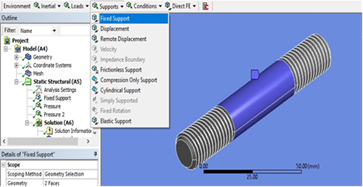
Figura 8. Condiciones de frontera del modelo.
Las condiciones de fronteras se establecieron para evitar movimientos de sólido rígido y poder estimar el estado de deformaciones y tensiones producidas por las cargas externas aplicadas sobre el sistema, se hizo necesario restringir el movimiento de parte de su dominio (u = 0 para el dominio Su). En este caso las fuerzas aplicadas fueron tratadas como cargas distribuidas sobre áreas pequeñas, pero finitas. Estas condiciones se definieron en el dominio ST.
En estas condiciones de frontera se consideró que, el momento torsor umbral está definido como el valor frontera entre el régimen elástico y el plástico del modelo. Se determinó la forma en que estarán conectados entre sí los elementos contiguos (a través de un nudo rígido o permitiendo algún tipo de deformación relativa), definiéndose, además, sus respectivas condiciones de apoyo (empotramiento, articulación o simple apoyo).
Para un modelo con acciones impuestas se establecieron aquellas que afectan a la estructura para una condición dada de funcionamiento, representadas por conjuntos de cargas o de deformaciones impuestas, tanto internas como externas, que se producen sobre el tornillo en estados de esfuerzos y de deformaciones. Se definió la carga a la que estará sometida el modelo y sin salir de Static Structural (A5), en el comando Loads>>Pressure, se asignaron las mismas. En la figura 9 se muestra el procedimiento.

Figura 9. Asignación de cargas al modelo.
Para la asignación de las cargas, el tornillo se consideró como un cuerpo tridimensional sometido a cargas y presiones, donde cualquier punto en este cuerpo está definido por las coordenadas x, y, z. La superficie o frontera está restringida a una región, donde el desplazamiento está especificado. En este caso se introduce una fuerza, la cual será bloqueada en las sucesivas etapas de carga, de manera que los efectos producidos inicialmente por dicha fuerza son preservados como desplazamientos después del bloqueo de la misma.
Se consideró este procedimiento, teniendo en cuenta que, de esta manera, se pueden reproducir las fuerzas de colapso y los distintos modos de fallo que aparecen en la unión. También se pueden obtener las tensiones, deformaciones y desplazamientos en los puntos que se deseen para poder crear curvas fuerza-desplazamiento o tensión-deformación como las que se obtienen en un ensayo real.
Resultados y discusión
La falla más común en pernos es fractura por fatiga, la parte más común donde se presenta es el primer hilo de cabeza-al pie, debido a que presenta mayor concentración de carga. Este tipo de falla generalmente se presenta por esfuerzos elevados anormales de esfuerzo, pernos que ya vienen con defectos de grietas, picaduras, ranuras y por esta razón se cumple esta falla. La generatriz, con un valor de 2,385 mm que se genera entre el espárrago y la tuerca, y considerando un Mext de 0,5 Nm que actúa sobre el espárrago del motor, la misma es de 1 367 Nm2.
Al someter el conjunto espárrago-tuerca a esta fuerza tangencial y ambos tener un comportamiento dúctil, con efecto de tensión, en un área como la de la culata del motor, expuesto a temperatura y vibraciones, entonces el límite de fluencia y de ruptura pueden ser afectados, independientemente que la misma sea uniformemente distribuida en el área de las roscas, se encargará de generar una fuerza de fricción que está relacionada también con el coeficiente de fricción del acero AISI 4140.
En la interfase entre dos piezas en contacto bajo presión (espárrago-tuerca), se producen movimientos relativos oscilatorios de pequeña amplitud que generan en la zona de contacto unas tensiones tangenciales asociadas a las normales en la superficie. Estas tensiones locales se suman a las globales de todo el componente, produciendo un efecto similar al de los concentradores de tensión.
Se determina el momento torsor al cual está expuesto el conjunto, en correspondencia con el tamaño crítico de las grietas y el esfuerzo aplicado.
Referencias bibliográficas
Arroyo, B.; Álvarez, J. (2017). Análisis de pernos galvanizados de alta resistencia utilizados en torres metálicas. Anales de Mecánica de la Fractura, 34(3), 95-105.
Bickford, J. (2007). An Introduction to the Design and Behavior of Bolted Joints, CRC Press.
Budynas, G. (2008). Diseño en Ingeniería mecánica de Shigley. McGraw-Hill.
Bursi, O. & Jaspar, J. (1997). Calibración de un modelo de elementos finitos para conexiones de acero con placa terminal atornillada aislada. Revista de investigación del acero para la construcción, 44(3), 225-262. https://www.sciencedirect.com/science/article/abs/pii/S0143974X97000564#scren-reader-main-content
Callister, W. (2006). Introducción a la Ciencia e ingeniería de los materiales. Reverté S. A.
Gainza-Legrá, A. (2016). Análisis de rotura del espárrago situado en el cárter de los motores MAN de la unidad empresarial de base generación motores FUEL-OIL de Moa. (Trabajo de Diploma, Universidad de Moa).
Guerra, Y., Ordoñez, U. & González, V. (2019). Análisis de la falla de pernos de fijación de las zapatas polares de un motogenerador. Ingeniería Mecánica, 22(3),156-160. https://www.redalyc.org/journal/2251/225160761006/movil/.
Hudgins, A. & James, B. (2014). Fatigue of threaded fasteners. Advance Materials and Processes, 172(8), 18-22. https://dl.asminternational.org/amp-tech/article-abstract/172/8/18/27806/Fatigue-of-Threaded-Fasteners?redirectedfrom=PDF.
Irwin, G. (1997). Plastic zone near a crack and fracture toughness. Sagamore Research Conference Proceedings.
Kulak, G. (1994). Fatiga de conexiones pernodas. Actas: Conferencia internacional sobre Fatigue, Toronto, Ontario. Sociedad Estadounidense de Soldadura.
Pero-Sanz, J., González, J. (2002). Solidificación y transformaciones en el sistema Fe-C-Cr. Bases para el diseño por propiedades de sus aceros y fundiciones Ternarias. RDM: Revista de Minas, (9), 81-92. https://dialnet.uniroja.es/servlet/articulo?codigo=4701975.