Ciencia & Futuro
V. 14. No.3 septiembre-noviembre 2024
ISSN: 2306-823X
Recibido: 3/04/2024/Aceptado: 20/07/2024
Cálculo de fractura en un tornillo de motor de combustión interna
Fracture calculation in an internal combustion engine screw
Lisander Romero Breffe lromerob@ismm.edu.cu (1)
Daniela García Torres dgarciat@ismm.edu.cu (1)
(1) Universidad de Moa, Cuba
Resumen: Se determinó la falla de un tornillo fabricado de acero AISI 4140 empleado en la culata de un motor de combustión interna a través de la mecánica de fractura. Para las cargas aplicadas sobre el tornillo se observa que cuando esta alcanza un valor de 2 056 565,96 N, entonces la carga axial teórica a la que está expuesto el perno es de 513 296,05 N; donde va a incidir con mayor influencia en un tamaño crítico de grieta de 6,2 mm. La carga se distribuye principalmente en las primeras tres cuerdas donde la primera ocupa alrededor del 55 % de la carga, la segunda el 25 % y la tercera el 15%; la tensión máxima en el tornillo es de 1 796 MPa.
Palabras clave: aleaciones, falla mecánica, fisuras, fractura por fatiga, motor térmico
Abstract: The failure of a screw made of AISI 4140 steel used in the cylinder head of an internal combustion engine was determined through fracture mechanics. For the loads applied to the screw, it is observed that when this reaches a value of 2,056,565.96 N, then the theoretical axial load to which the bolt is exposed is 513,296.05 N; where it will have the greatest influence on a critical crack size of 6,2 mm. The load is distributed mainly on the first three ropes where the first occupies about 55% of the load, the second 25% and the third 15%; the maximum stress in the screw is 1 796 MPa.
Keywords: alloys, mechanical failure, cracks, fatigue fracture, heat engine
Introducción
Los sistemas mecánicos están sometidos durante su funcionamiento a cargas variables. La aplicación prolongada de estas cargas puede dar lugar a la aparición de fisuras en el material, por lo general en la superficie, que evolucionan a través de él, disminuyendo la capacidad de carga del componente y pudiendo culminar en su fractura. Este fenómeno es conocido como falla por fatiga y es responsable de más del 50 % de las fallas en componentes mecánicos en servicio (Campbell, 2012).
El desarrollo de la mecánica de fractura se basa en tres factores principales que controlan la susceptibilidad de una estructura a la fractura frágil. Estos son: la tenacidad de fractura del material, medida de la fisura, y nivel de esfuerzo aplicado. La tenacidad de fractura puede ser definida como la capacidad del material de soportar carga o deformación plástica en presencia de una grieta, este parámetro es considerado el más importante en el estudio de la mecánica de fractura de un material por dos razones (Zamanzadeh et al., 2015).
El acero AISI 4140 tiene diversas aplicaciones y es uno de los materiales más utilizados para el diseño y fabricación de máquinas (Romero & Rondón, 2019; Ramírez et al., 2023). Muestra una alta resistencia a la tracción, sin embargo, presenta baja resistencia al desgaste y a la corrosión por lo que se puede ver restringida su vida útil (Correa et al., 2008).
Este trabajo propone determinar la falla de un tornillo fabricado de acero AISI 4140 empleado en la culata de un motor de combustión interna a través de la mecánica de fractura.
Materiales y métodos
Modelo para el análisis tenso deformacional del tornillo
Se realizó el análisis tenso deformacional originado en un tornillo como consecuencia de la unión tornillo-tuerca. Para materiales que presentan un comportamiento elástico lineal, la relación esfuerzo deformación se define por la ley de Hooke. En el caso particular de trabajar con materiales isótropos, las constantes elásticas que caracterizan su comportamiento mecánico son; el módulo de Young o de elasticidad (E) y el módulo de Poisson (v).
Para obtener el valor de la fuerza tangencial distribuida en el área total de la rosca que relaciona el momento exterior aplicado y la fuerza tangencial se considera la ecuación:
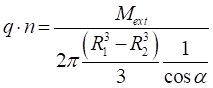
Donde:
q: fuerza tangencial; N/m2
n: número de roscas
Mext: momento exterior en la base del tornillo; N/m
R1: Radio exterior de la rosca, m
R2: Radio interior de la rosca, mm
Queda definido como: 
Para obtener la ecuación se tuvo en cuenta el área de la rosca en la que actúa la fuerza distribuida, es un área de cono de ángulo 45º como se muestra en la figura 1.
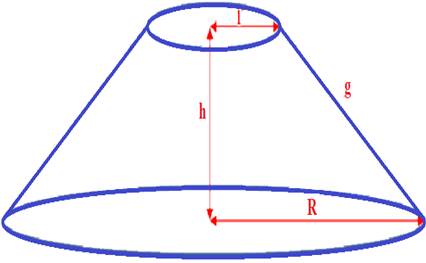
Figura 1. Tronco de cono.
El tronco de cono con bases paralelas, queda definido por los parámetros que se muestran en la figura 2.
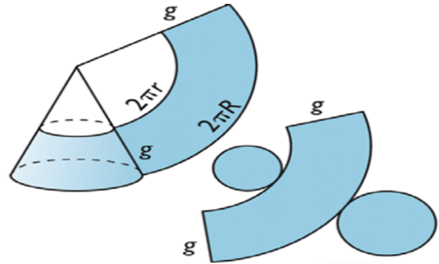
Figura 2. Desarrollo del tronco de cono (Bickford, 2007).
Donde:
r: radio de la base menor, mm
R: radio de la base mayor, mm
h: altura, mm
g: generatriz, se calcula mediante la ecuación:
g2 =(R-r)2 + h2
Para calcular el momento torsor (Mtor) en una rosca, se ha tenido en cuenta el momento torsor sobre un anillo circular. El momento se calcula como:
Mtor= Fza·distancia
La fuerza distribuida actúa sobre el área de la rosca, se define como:
Fza = Fza distribuida · Área
El área real en el que actúa la fuerza distribuida, es un tronco de cono, el área de un anillo circular y un tronco de cono y se determina:
El anillo circular es la proyección del área del tronco de cono, como muestra la figura 3.
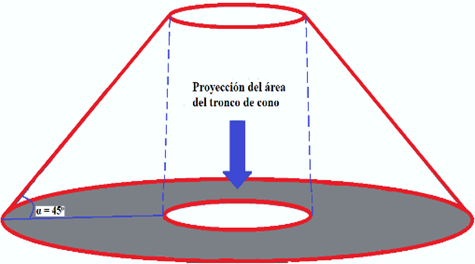
Figura 3. Proyección del área del tronco de cono (Shigley y Mischke, 1998).
Para el cálculo se considera un elemento diferencial de un anillo circular, como se muestra en la figura 4.
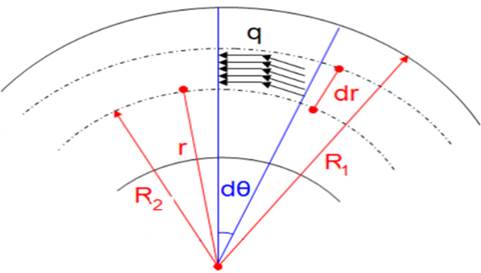
Figura 4. Elemento diferencial de un anillo circular (Shigley y Mischke, 1998).
Entonces el momento torsor se calcula como:
Donde:
rdJ·dr: área del anillo circular
r: distancia al eje z, eje desde el cuál se obtiene el momento torsor
Sustituyendo la ecuación se obtiene:
El momento calculado es el correspondiente a una rosca del modelo, para el conjunto total de roscas es:
De la ecuación anterior, se puede obtener la Fzadistribuida que hay que aplicar al modelo:
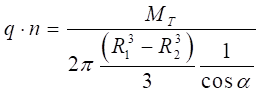
Determinación de la falla en el tornillo
Para la evaluación de defectos, tanto fisuras como entallas, así como la interacción de cavidades detectadas en los anclajes se utilizaron los diagramas de evaluación de falla de acuerdo con el procedimiento y reglas de interacción de la BS 7910 (2005). El concepto del factor de intensidad de esfuerzos para la modelación del momento tenso deformacional del tornillo, puede determinarse según Irwin (1961) como:
Donde la variable Y es el factor geométrico el cual depende de la forma de la pieza, σ es el esfuerzo aplicado y a es el tamaño de la grieta. En la tabla 1 se muestran los resultados obtenidos, tanto para el esfuerzo aplicado, como para el factor de intensidad de tensiones.
Tabla 1. Esfuerzo aplicado y factor de intensidad de tensiones
|
Para Y = 1,1 |
Esfuerzo aplicado (MPa) |
Factor de intensidad |
|
KI1 |
297,74 |
94,028 |
|
KI2 |
311,28 |
119,438 |
|
KI3 |
289,95 |
127,163 |
|
KI4 |
270,21 |
193,519 |
Donde σ es una tensión con diferentes valores y depende del sistema de cargas.
Diámetro máximo: 56 mm
Diámetro mínimo: 53,4 mm
Radio de fondo: 52,4 mm
Paso de la rosca: 4 mm
El modelo de la figura 5 fue el considerado para realizar los cálculos.
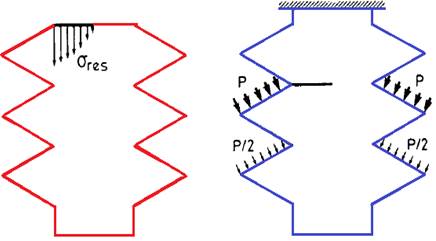
Figura 5. Condiciones de carga. a) Tensiones residuales. b) Carga debida a la tuerca.
La carga ha sido aplicada directamente en la rosca debida a la tuerca. El diseño se ha realizado, según consideraciones de Schnack (1980) quien consideran la distribución de tensiones a lo largo de las superficies de rosca de un tornillo. De acuerdo con estas referencias, el sistema de cargas consiste en una presión uniforme aplicada directamente sobre los filetes de roscas situados inmediatamente debajo de la fisura, con un valor p sobre el primer filete (el más próximo a la fisura) y la mitad de ese valor (p/2) sobre el segundo filete (debajo del primero).
Para la carga axial, σ que es la tensión axial remota en la sección neta del tornillo (distribución uniforme de tensiones):
En el caso del momento flector, σ representa la máxima tensión axial en la sección neta del tornillo (distribución triangular de tensiones):
En el caso de carga producida por la tuerca, σ; es la tensión neta en la dirección axial.
Donde
FTOTz: carga total en dirección del eje del tornillo.
Los
esfuerzos en la punta de la grieta presentan una singularidad 
, ello implica que los
esfuerzos tienden al infinito, debido a que los materiales estructurales se
deforman plásticamente. Por lo anterior, el análisis elástico no es aplicable.
La formación de la zona plástica puede ser considerada como una perturbación a
la solución elástica y es necesario realizar la corrección correspondiente, se
determina según Albañil y Mora (2002) como:
Resolviendo para r:
Donde σy es el límite elástico del material.
Para determinar la carga de trabajo del tornillo se considera que la misma es aplicada directamente a los elementos roscados y que los mismos estuvieran igualmente cargados. De acuerdo con Dobrovolski (1991) se determina como:
Donde:
P: carga de trabajo
D: diámetro de la tapa del cárter del motor; mm
Z: cantidad de espárragos
p: presión interna de la tapa del cárter del motor; MPa
Se determinó la fuerza residual de tensado de acuerdo con la magnitud de la carga de trabajo por la ecuación:
V = P· g
Donde:
V: tensado residual;
g: coeficiente experimental.
Se considera en los cálculos de 0,2 a 1,8; según sean las condiciones de trabajo del conjunto.
La carga axial teórica se determinó a partir de la condición de equilibrio, la fuerza que recae sobre el espárrago es igual a la suma de la carga de trabajo y la fuerza residual de tensado.
P0=P+V=P(1+g)
Donde:
P0: carga axial teórica; N
La presencia del desgarramiento en los filetes de la rosca del agujero, sugiere que fue superada la resistencia al corte de los mismos. Para verificar lo anterior se procedió a realizar un cálculo aproximado. La carga producida por el apriete sobre el tornillo y por lo tanto sobre el agujero, estará dada según Kulak (1994) por:
Donde:
Ptor: carga aplicada sobre el tornillo
dp: diámetro de paso; mm
a: ángulo de cara de rosca; grado,
L: avance; mm
μ: coeficiente de fricción.
El área de los filetes que soportó la carga en el agujero es:
A=p·d·w·Pros·Nf
Donde:
A: área cortante de los filetes roscados; mm2
w: factor de corrección por juego entre roscas (0,88)
Pros: paso de rosca; mm
Nf: número de filetes roscados.
El esfuerzo cortante que soportaron los filetes:
Para obtener el valor de la fuerza tangencial distribuida en el área total de la rosca, se aplica la ecuación siguiente, que relaciona el momento exterior aplicado y dicha fuerza tangencial:
Donde:
q: fuerza tangencial; N/m2
n: número de roscas
R1: radio interior de la rosca; mm
R2: radio exterior de la rosca; mm
Resultados y discusión
Comportamiento tenso deformacional del tornillo fisurado
La falla más común en pernos es fractura por fatiga, la parte más común donde se presenta es el primer hilo de cabeza al pie, debido a que presenta mayor concentración de carga. Este tipo de falla generalmente se presenta por esfuerzos elevados anormales de esfuerzo, pernos que ya vienen con defectos de grietas, picaduras, ranuras y por esta razón se cumple esta falla. Para determinar la fuerza tangencial distribuida en el área total de la rosca se consideró la ecuación 1, determinando la generatriz por la ecuación 2 con un valor de 2,385 mm que se genera entre el espárrago y la tuerca, y considerando un Mext de 0,5 Nm que actúa sobre el espárrago del motor, la misma es de 1 367 Nm2.
En este elemento roscado comienza a ser concluyente el tamaño crítico de la grieta (~ 12 mm) en el diámetro del tornillo y a la falla del mismo a partir de un Mtor de 13 417 Nm y de un esfuerzo de 778,2 Nm2. Cuando sobre el tornillo de acero AISI 4140 se ejerce una fuerza de 297 918,52 N da inicio a cambiar el límite elástico de este acero con la propagación de grietas, sin embargo, esta acción combinada tiene efecto desde el inicio de la grieta hasta un valor de 6,2 mm, a partir del cual este fenómeno tiene lugar en la zona de transición entre las deformaciones elásticas y plásticas y se caracteriza por un rápido incremento de la deformación sin aumento apreciable de la carga aplicada.
En el acero AISI 4140, para las cargas aplicadas sobre el tornillo se observa que, cuando esta alcanza un valor de 2 056 565,96 N, entonces la carga axial teórica a la que está expuesto el perno y soporta el mismo va a ser de 513 296,05 N; donde va a incidir con mayor influencia en un tamaño crítico de grieta de 6,2 mm. Si se considera entonces la tensión última del perno que es de 663,29 MPa a una temperatura de 600 oC, este tornillo sometido a un estado de cargas sufre deformaciones que dan lugar a un estado tensional, existiendo una respuesta deformacional del material debido a sus propiedades mecánicas.
Conclusiones
Se determinaron las tensiones que se originan en un tornillo fabricado de acero AISI 4140 empleado en la culata de un motor de combustión interna mediante el método de la mecánica de fractura.
Se determinó que, para las cargas de 2 056 565,96 N, entonces la carga axial teórica a la que está expuesto el perno va a ser de 513 296,05 N.
Referencias bibliográficas
Albañil, H.& Mora, E. (2002). Mecánica de Fractura y Análisis de Falla. Editorial UN.
Bickford, J. (2007). An Introduction to the Design and Behavior of Bolted Joints. CRC Press, USA.
BS 7910 (2005). Guide to methods for assessing the acceptability of flaws in metallic structures. https://knowledge.bsigroup.com/products/guide-to-methods-for-assessing-the-acceptability-of-flaws-in-metallic-structures-1/standard
Campbell, F. (2012). Fatigue and Fracture: Understanding the Basics. ASM International.
Correa, F., Caicedo, J.C., Aperador, W., Rincón, C.A. & Bejarano, G. (2008). Mejoramiento de la resistencia a la corrosión del acero AISI 4140 utilizando multicapas de titanio. Revista de la facultad de ingeniería de la Universidad de Antioquia, (46), 7-14. http://redalyc.org/articulo.oa?id=43004602
Dobrovolski, V. (1991). Elementos de máquinas. Mir.
Irwin, G. (1961). Plastic zone near a crack and fracture toughness. Sagamore Research Conference Proceedings.
Kulak, G. (1994). Fatigue of bolted connection. The International Conference on Fatigue, American Welding Society.
Ramírez, L., Toapanta, L. A., Simbaña, Á. & Guilcaso, C.O. (2023). Análisis de rugosidad del Acero AISI 4140 tratado térmicamente y mecanizado CNC. Revista científica multidisciplinar G-nerando, 4(1), https://revista.gnerando.org/revista/index.php/RCMG/article/view/115
Romero, J. & Rondón, E. (2019). Rolling friction oh AISI 4140 steel in a ring on ring tribometer. Revista ingeniería UC, 26(2), 185-191. https://redalyc.org/articulo.oa?id=70760276007
Schnack, E. (1980). Genaue kerbspannungs analyse von Zchrauben-Mutter verbindungen. VDIZ, 122(11), 101-109. https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=PASCL8130010893
Shigley, J. & Mischke, C. (1998). Diseño en Ingeniería Mecánica. McGraw Hill.
Zamanzadeh, M., Larkin, E. & Mirshams, R. (2015). Fatigue failure analysis case studies. Journal of Failure Analysis and Prevention, 15(6), 803-809. https://idp.springer.com/article10.1007/s1169-015-0044-3