Ciencia & Futuro 

V. 15. No.3 septiembre-noviembre 2025

ISSN: 2306-823X

Recibido: 28/4/2025/Aceptado: 13/7/2025

Determinación de las tensiones en una placa de acero estructural AISI 1045 mediante elementos finitos

Determination of stress in an AISI 1045 structural steel plate using finite elements

Lisander Romero Breffe lromerob@ismm.edu.cu ⁽¹⁾

https://orcid.org/0009-0009-1791-0071

Leodenis Santi García leosantigarcia91@gmail.com ⁽¹⁾

https://orcid.org/0009-0007-8356-8433

⁽¹⁾ Universidad de Moa, Moa, Cuba

Resumen: El trabajo tiene como objetivo determinar a través del Método de los Elementos Finitos, las tensiones que se originan en una placa fabricada de acero estructural AISI 1045. Para la determinación de las tensiones se empleó el software ANSYS 17.2, a través del cual se realizó la modelización geométrica y parametrizada, el mallado de la placa y la definición de los casos de carga y de sus parámetros, así como las condiciones de frontera del modelo. Se determinó que, la tensión de Von Mises es de 50,295 MPa; además según los resultados obtenidos el desplazamiento total ocurre a un valor de 0,021181 mm.

Palabras clave: método numérico, aleación metálica, modelación tridimensional

Abstract: The objective of the work is to determine, through the Finite Element Method, the stresses that originate in a plate made of AISI 1045 structural steel. To determine the stresses, the ANSYS 17.2 software was used, through which the geometric and parameterized modeling, meshing of the plate and the definition of the load cases and their parameters, as well as the boundary conditions of the model. It was determined that the Von Misses stress is 50.295 MPa; furthermore, according to the results obtained, the total displacement occurs at a value of 0.021181 mm.

Key words: numerical method, metal alloy, three-dimensional model

Introducción

Baran (1989) define el análisis por Elementos Finitos (EF) como un grupo de métodos numéricos para la aproximación de las ecuaciones que gobiernan cualquier sistema continuo. El principio de los EF, es una teoría matemática basada sobre los cálculos de las variaciones, teoremas energéticos, el principio de elasticidad y ecuaciones de la física y la ingeniería (Benito Muñoz et al., 2023). La principal función de un programa de EF es reducir la ecuación diferencial a un sistema de ecuaciones algebraicas simultáneas las cuales pueden resolverse por la computadora, como la ecuación diferencial parcial de segundo orden de Poisson (Felix, Nogueira & Maíz, 2023; Mausa, 2024), la cual gobierna las deflexiones de una membrana en una viga prismática flexionada y la conducción del calor con su fuente.

El alcance del método se considera amplio (Otero et al., 2021; Cangelosi & Sanzi, 2022; Castillo, 2025). La representación analítica significa la habilidad para combinar, en un modelo simple con diferentes procedimientos de los modelos, cada tipo de elemento, siendo descrito por una ecuación diferencial, ya explicado. La capacidad de representación geométrica es generalmente observada como la primera ventaja del método. Los elementos triangulares pueden arreglarse en cualquier manera deseada para aproximar la forma de la estructura o cuerpo, en el plano o en el espacio (Ramos et al., 2009).

Modelos de elementos finitos en dos dimensiones (2D) vs tridimensionales (3D)

En las décadas del 70 y el 80 la modelación de piezas se realizó mediante modelos simplificados en dos dimensiones, debido a las limitaciones computacionales de aquellos momentos. La modelación en 2D tiene como ventaja que produce modelos más sencillos y reduce grandemente el tiempo de cálculo, conduciendo en ocasiones a resultados aceptables. Hibbitt y Marcal (1973) fueron pioneros en la aplicación de un modelo 2D para la determinación de tensiones residuales. En la actualidad, a pesar de los avances computacionales muchos autores continúan trabajando la modelación en 2D con modelos planos o axisimétricos y asumiendo determinadas suposiciones y simplificaciones (Siddique et al., 2005; Ferro, Bonollo & Tiziani, 2010; Moreira, Lopes & Sanches, 2023).

Autores como Mercado Bautista (2020), Sánchez et al. (2022); Quirón Avendaño & Cruz Zuñiga, (2024) Lorza et al. (2023); Estrada Garibay et al. (2024), validan la eficacia de la modelación 3d y su aplicabilidad en diversas esferas técnicas para la solución de problemas. Siddique et al. (2005) Bezerra, Rade & Scotti (2006) reportan que la respuesta térmica y termodeformacional de todos los conjuntos es tridimensional y que solo estos modelos son capaces de reproducir completamente el fenómeno termodeformacional. Lu y Hassan (2001) han empleado la modelación tridimensional para la simulación de una pieza mecánica de cuatro pasadas mediante un modelo 3D. Refiere que, en los puntos de inicio y fin de la soldadura se observa una alta concentración de tensiones residuales de tracción y compresión que no puede ser recogida por los modelos bidimensionales.

Cuando se realiza un modelo se debe recurrir al análisis de la convergencia para seleccionar el tamaño correcto de los elementos en el mallado y, de este modo, obtener el mínimo de error en los resultados. La convergencia define que, al refinar progresivamente la malla, la solución numérica se aproxima, tanto como se desee, a la solución exacta del fenómeno.

Este es un factor que debe garantizar que los resultados del cálculo no dependan de la densidad del mallado (Goldak y Moashi, 1999; García y Bejar, 2003). Como método de solución aproximada se puede plantear entonces que los paquetes MEF posibilitan encontrar las magnitudes desconocidas en determinados puntos y con determinada cercanía a la solución exacta, precisión que, como se ha mencionado, mejora con el aumento del número de elementos, es decir, aumentando la densidad de mallado.

Materiales y métodos

Modelado de las tensiones por elementos finitos

El modelo FEM propuesto se define automáticamente a partir de un fichero de trabajo programado en lenguaje PCL (Patran Command Language), sujeto a comandos especiales de MSC. El modelo FEM resultante de la ejecución de este fichero contiene las características principales siguientes:

1. Modelización geométrica y parametrizada, que permite definir la disposición matricial de las placas, métricas y dimensiones principales de las placas como el usuario decida.

2. Mallado automático de las placas. Para las placas, elementos viga según formulación Euler-Bernoulli.

3. Definición automática de los casos de carga y de todos los parámetros de cálculo necesarios para la generación del fichero de entrada al programa de cálculo.

El fichero de texto generado es ejecutado por el usuario en el solver de elementos finitos utilizado, en este caso, MSC.NASTRAN. Finalmente, los resultados se muestran en el post-procesador, de manera que puede realizarse un tratamiento de todos los datos que se consideren interesantes (tensiones, deformaciones del sistema, separaciones puntuales de contactos). La modelación mediante ANSYS consta de tres etapas fundamentales: a) etapa de preprocesamiento, b) de solución y c) de postprocesamiento. La presente metodología (Carnicero, 2001), considera los modos de trabajo, la interface gráfica del usuario y el modo por bloques de programación ordenados. En la figura 1 se muestra la interfaz gráfica del usuario

Figura 1. Interface del usuario.

Al ejecutar el software, se cierra la ventana que tiene por título Welcome to ANSYS Workbench y se selecciona el análisis a realizar, se escoge el que se muestra resaltado en color rojo, que es un análisis estático (Static Structural). En el toolbox identificado se hará doble clic y se visualiza lo que se muestra en la pantalla de la figura 2.

Figura 2. Selección del tipo de análisis.

Este análisis se realizó fundamentalmente en modo de programación.

-Se declaró como tipo de análisis el “estático”.

-Se empleó el método iterativo de solución de ecuaciones no lineales “FULL NEWTON RAPHSON”, que constituye el método no lineal estándar de ANSYS para problemas de plasticidad.

En el proceso de simulación, tras haber definido el material y sus propiedades y haber generado la geometría, se procede a construir la malla con el tipo de elemento elegido asociada a esa geometría. Para ello se debe especificar el tamaño medio del elemento, que podrá reducirse posteriormente. Se ejecuta un clic derecho sobre la palabra mesh>>Generate Mesh, obteniéndose el modelo mallado mostrado en la figura 3.

Figura 3. Generación y mallado del modelo.

Debido a que los esfuerzos y deformaciones van a presentar mayores cambios en el agujero, resulta muy útil utilizar una malla fina únicamente cerca de esta zona. Al estar empleando el método-h de resolución, en la malla van a poder coexistir diferentes tamaños de elemento, con lo que se logra exactitud y resolución con ajuste de los costos computacionales adicionales. Así, las áreas del acero AISI 1045 contarán con una malla relativamente gruesa que será refinada cerca del agujero, donde los elementos de mallado serán mucho menores.

Para el mallado el modelo se procede a establecer las condiciones de frontera, ejecutando el comando Supports>>Fix Supports como se muestra en la figura 4.

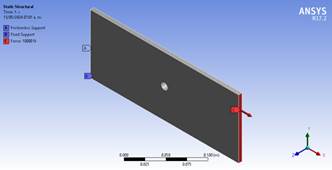
Figura 4. Condiciones de frontera del modelo.

Las condiciones de fronteras se establecieron para evitar movimientos de sólido rígido y poder estimar el estado de deformaciones y tensiones producidas por las cargas externas aplicadas sobre el sistema, se hizo necesario restringir el movimiento de parte de su dominio (u = 0 para el dominio Su). En este caso las fuerzas aplicadas fueron tratadas como una carga distribuida sobre el área de la cara en color rojo. Estas condiciones se definieron en el dominio ST.

Resultados y discusión

Análisis por el Método de los Elementos Finitos

Una forma de caracterizar las propiedades plásticas del acero es a través del modelo mecánico de Johnson-Cook, que reproduce el comportamiento de los materiales sujetos a grandes deformaciones, altas temperaturas y altas velocidades de deformación. La formulación de este modelo define la tensión equivalente de Von Mises, como tres términos desacoplados donde el primero de ellos define la dependencia del endurecimiento por deformación, el segundo la sensibilidad de la deformación y el tercero la sensibilidad de la temperatura. En la figura 5 se muestra el análisis de las tensiones a las cuales está sometida la placa.

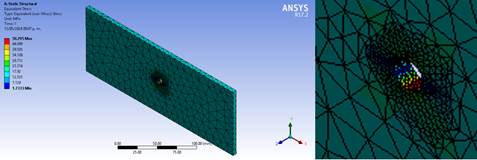
Figura 5. a) Tensión máxima equivalente de Von Mises. b) Agujero.

En esta situación la placa actúa en condiciones rígidas y se puede observar que, la distribución de la tensión de Von Mises, las zonas más críticas se producen en el agujero (Figura 5b), se determina que la tensión máxima en la placa de acero estructural AISI 1045 es de 50,295 MPa.

La deformación del material ocurre debido al comportamiento elástico, donde el crecimiento de la curva es lineal hasta que se produce la rotura. A partir de este momento, la deformación vuelve a cero y empieza a aumentar linealmente hasta que se hace constante (tensión constante). En la figura 6 se muestra la deformación total de la placa fabricada de acero estructural AISI 1045.

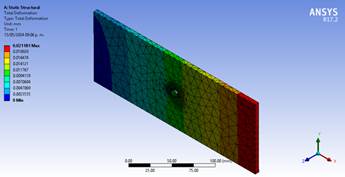
Figura 6. Deformación total.

Se muestra el mapa de deformación que ha sufrido el material en el primer extremo (zona roja), ya que es la que sufre mayores deformaciones. Según los resultados obtenidos de la deformación total de 0,021181 mm se observa que, la carga se distribuye principalmente en los primeros tres de la placa donde la primera ocupa alrededor del 55 % de la carga, la segunda el 25 % y la tercera el 15%. León et al. (2001) han expuestos que, la distribución teórica sugiere que la mayoría de las fallas se presentarían en la primera cuerda, demostraron además que, el 90 % de las fallas se presentaron en la primera cuerda al ser sometidos a una carga axial.

Determinada la distribución de la carga en contacto con la placa, se determinó la intensidad de esfuerzo. En la figura 7 se muestra el resultado obtenido de este análisis.

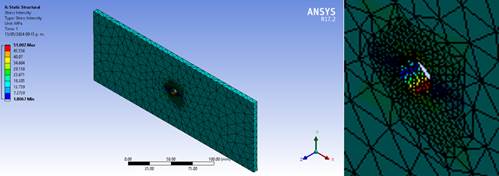
Figura 7. a) Intensidad de tensiones en el modelo. b) Zona de máxima intensidad.

Se observa que, la intensidad de tensiones se encuentra en el agujero (Figura 7b), con un resultado de 51,002 MPa aunque la distribución de este esfuerzo es irregular debido a que existen dos factores que contribuyen al estado de esfuerzo en esa zona: el estiramiento de la placa bajo la carga axial y la flexión en la zona de contacto. La magnitud del esfuerzo bajo solo la carga axial se determinó utilizando el concentrador de esfuerzo propuesto por Neuber y propuesto por Pilkey y Pilkey (2020) con un factor de corrección propuesto por Dragoni, asumiendo que se comporta como una muesca periódica en una placa.

Conclusiones

Se determinaron las tensiones que se originan en una placa fabricada de acero estructural AISI 1045 mediante el método de los elementos finitos.

Se determinó que las tensiones en la placa pueden ser influenciadas por diversos factores como la geometría, la carga aplicada y las propiedades del material utilizado en la fabricación.

La tensión máxima equivalente de Von Mises a la cual está expuesta la placa es de 50,295 MPa, lo que indica que el componente está sometido a cargas significativas y puede estar en riesgo de falla por fractura.

Referencias bibliográficas

Baran, N. (1989). Finite Analysis on Microcomputers. McGraw-Hill book Company.

Benito Muñoz, J.J., Salete Casino, E., Álvarez Cabal, R., Ureña Prieto, F. & Flores Escribano, J. (2023). Introducción al método de los elementos finitos. Editorial UNED.

Bezerra, A., Rade, D. & Scotti, A. (2006). Simulation of a TIG weld using finite element method: Part 1 Thermal Analysis. Soldagem & Insecaop, 11(1), 12-22.

Cangelosi, C.G. & Sanzi, H.C. (2022). Análisis termomecánico de un reactor mediante el método de diferencias finitas y su verificación a partir del método de los elementos finitos. Revista Iberoamericana de Ingeniería Mecánica, 26(1), 25-41. https://revista.uned.es/universidad/dam/facultades/industriales/RIBIM/V26N1Abril2022/26N1Ab20200-A04.pdf

Carnicero, A. (2001). Introducción al método de los elementos finitos. Escuela Técnica Superior de Ingeniería ICAI. Universidad Pontificia Comillas, Madrid.

Castillo, J.C. (2025). Ecuaciones Diferenciales: Fundamentos. Método de Solución y Aplicaciones en Sistémicas Dinámicos y Teoría del caos. Ibero ciencias. Revista Científica Académica, 4(2), 1-21. https://revistaiberociencias.org/index.php/multidisciplinar/aticle/view/35

Estrada-Garibay, J.A., Vázquez-Martínez, B., Castillo-González, D.J. & Ochoa-Almazán, D.E. (2024). Prototipo de dispensador automático para la optimización de ventas en diferentes sectores. Revista De Ciencias Tecnológicas, 7(3). https://doi.org/10.37636/recit.v7n3e358

Felix, D. H., Nogueira, S. F., & Maíz, S. (2023). Análisis del Efecto Poisson en las Vibraciones Naturales de Microvigas Timoshenko Mediante el Método de Elementos Finitos. Mecánica Computacional, 40(5), 131-140. https://amcaonline.org.ar/ojs/index.php/mc/article/view/6533

Ferro, P., Bonollo, F. & Tiziani, A. (2010). Metodologías y validaciones experimentales de la simulación numérica del proceso de soldadura. Revista Internacional de Ciencia Computacional de Materiales e Ingeniería de superficies, 3(2-3), 114-132. https://doi.org/10.1504/IJCMSSE.2010.033148

García, Y. & Bejar, A. (Noviembre 2003). Obtención de los campos térmicos mediante el Método de los Elementos Finitos en las reparaciones por soldadura en equipo o estructuras metálicas de gran importancia. XXV Congreso Internacional de Metalurgia y Materiales. Instituto Tecnológico de Saltillo, México.

Goldak, J. & Moashi, G. (1999). Numerical Aspect of modelling Weld. Carleton University. ASM Handbook, Vol 6 Welding, Brazing and Soldering.

Hibbitt, H. & Marcal, P. (1973). A numerical thermo-mechanical model of the welding and subsequent loading of a fabricated structure. Computadoras y Estructuras, 3(5), 1145-1174. https://doi.org/10.1016/0045-7949(73)90043-6

Lorza, R.L., Martínez, A.P., Macedo, S.Í., Fraile, C.S., Gomez, F.S., Bobadilla, M.C.& González, S.R. (2023). Caracterización mecánica y térmica de Bronce-PLA fabricado mediante modelado por deposición fundida MDF. XXIV Congreso Nacional Ingeniería Mecánica (CNIM 2023). Libro de Resúmenes.

Lu, X. & Hassan, T. (2001). Residual Stresses in Butt and Socket Welded Joints. SMiRT, 16. https://repository.lib.ncsu.edu/server/api/core/bitstreams/034c9c28-0775-4171-ae54-3309d7f9fea8/content

Mausa, S. P. C. (2024). Solución numérica para las ecuaciones de Nernst-Planck-Poisson usando un Método de Elementos Finitos. (Tesis Doctoral, Universidad de Córdoba, Colombia). https://repositorio.unicordoba.edu.co/server/api/core/bitstreams/eda9be7a-f969-4e0b-97ac-1231e58057e6/content

Mercado Bautista, J.D. (2020). Evolución de los softwares de simulación para el Diseño y Construcción en la Industria. Polo del Conocimiento, 5(8), 1332-1343. https://dialnet.unirioja.es/servlet/articulo?codigo=7554321

Moreira, D. H. F. R., Lopes, W. C., & Sanches, R. A. K. (2023). Stable high order space-time finite element formulation for large displace-ment elastodynamics. XLIV Ibero-Latin American Congress on Computational Methods in Engineering, 5(05). https://publicacoes.softaliza.com.br/cilamce2023/article/download/5095/4173

Otero, P., Peñafiel, S., Vallejo, D., Granda, N. & Ramírez, J. (2021). Simulación de Mallas de Puesta a Tierra utilizando el Método de los Elementos Finitos en Tres Dimensiones. Revista Técnica Energía, 17(2), 113-123. https://doi.org/10.37116/revistaenergia.v17.n2.2021.437

Pilkey, W.D., Pilkey, D.F & Bi, Z. (2020). Factores de concentración de tensiones de Peterson. John Wiley & Sons.

Quirón Avendaño, L.A. & Cruz Zuñiga, N. (2024). BIM 6D methodology as a tool to evaluate thermal comfort in Costa Rican schools. Ingeniería, 35(1), 24-37. http://dx.doi.org/10.15517/ri.v35i1.60089

Ramos, F., Duffus, A., Rodríguez, M., Diaz, E. & Pozo, J. (2009). Influencia de la termodependencia de las propiedades físicas del acero en la simulación por elementos finitos del proceso de soldadura. Revista de la Facultad de Ingeniería de Antioquia, 48(4), 87-96. http://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=21411409

Sánchez, J.A., Sánchez, T.A., Gasca, A., Martínez, L.S., Núñez, K.N., Ruelas, M. & Sánchez, F. (2022). Simulación del esfuerzo mecánico en una pieza modelada en 3D por el método de los elementos finitos. Jóvenes en la Ciencia, 16, 1-10. https://www.jovenesenlaciencia.ugto.mx/index.php/jovenesenlaciencia/article/view/3567

Siddique, M., Abid, M., Junejo, H. & Mufti, A. (2005). 3-D finite element simulation of welding residual stresses in pipe-flange joints: effect of welding parameters. Materials Science Forum, (100), 79-84. https://doi.org/10.4028/www.scientific.net/MSF.490-491.79