Ciencia & Futuro 

V. 14. No.4 diciembre 2024-febrero 2025

ISSN: 2306-823X

Recibido:6/8/2024/Aceptado: 12/10/2024

Rediseño de instalación de hidrotransporte para el estudio del crudo cubano mejorado 650 en la Universidad de Moa

Redesign of hydrotransport facility for the study of improved cuban 650 crude oil at Moa University

Yasmani Romero Gé romerogeyasmani446@gmail.com ⁽¹⁾

Michel Rodríguez Ismar mrismar@ismm.edu.cu ⁽²⁾

Rodney Martínez Rojas rmartinez@ismm.edu.cu ⁽²⁾

Oscarina Barroso Romero oscarinabarroso002@gmail.com ⁽³⁾

⁽¹⁾ Empresa Niquelífera Moa Nickel, Cuba ⁽²⁾ Universidad de Moa, Cuba    

⁽³⁾ Empresa Mecánica del Níquel, Cuba

Resumen: Se realizó el rediseño de la instalación de hidrotransporte a escala experimental perteneciente al laboratorio de hidráulica en la Universidad de Moa, con vista al estudio del manejo de combustibles cubanos pesados como Crudo Mejorado 650. La evaluación del sistema de bombeo realizado en función de la característica reológica del fluido, permitió establecer la presión requerida de descarga de la bomba de 141 metros columna líquida, por debajo de la de diseño propuesta por el fabricante. Otro de los principales resultados fue la propuesta del espesor de aislamiento térmico de lana de vidrio, que permitiría una reducción en las pérdidas de energía de alrededor del 89,56 % en la instalación, además de la propuesta de selección del calentador a utilizar en el tanque del tipo de resistencia eléctrica marca Polimex.

Palabras claves: petróleo cubano, propiedades reológicas, transporte de fluido

Abstract: The redesign of the hydrotransport facility was carried out on an experimental scale belonging to the hydraulics laboratory at the University of Moa, with a view to the study of the management of heavy Cuban fuels such as Improved Crude 650. The evaluation of the pumping system carried out based on the rheological characteristic of the fluid made it possible to establish the required pump discharge pressure of 141 meters liquid column, below the design pressure proposed by the manufacturer. Another of the main results was the proposal for the thickness of glass wool thermal insulation, which would allow a reduction in energy losses of around 89.56% in the installation, in addition to the proposal for selecting the heater to be used in the Polimex brand electrical resistance type tank.

Keywords: Cuban oil, fluid transport, rheological properties

Introducción

La transportación de los combustibles en las centrales termoeléctricas cubanas y la industria minero metalúrgica, cobra importancia primaria en el trasiego por sistemas de tuberías desde los puertos hasta los depósitos y su posterior destino hacia las plantas. Estos sistemas difundidos mundialmente, cuando operan en los parámetros de máxima eficiencia, son de gran efectividad económica y ambiental con respecto a los demás medios de transporte de combustibles pesados (Laurencio et al., 2022).

Los petróleos crudos cubanos son fluidos de elevada viscosidad con comportamiento no newtoniano, que cambian esa propiedad en función del gradiente de velocidad, por lo que se requiere la determinación de modelos reológicos que describan su comportamiento de flujo (Laurencio & Delgado, 2008). El combustible cubano CM-650, formulado a partir de mezclas de petróleo crudo cubano de alta viscosidad presenta numerosas dificultades para su transporte y manejo, requiriéndose técnicas especiales. El calentamiento del combustible a una temperatura adecuada para el bombeo constituye la alternativa más usual y viable aplicada en la actualidad (Laurencio, 2012).

La instalación de un nuevo oleoducto requiere de estudios, en los cuales, se tienen en cuenta todas las variantes que pudieran beneficiar el transporte. El análisis permite detectar de forma preliminar las diferentes características y deficiencias que se manifiestan entre las investigaciones realizadas, las teorías existentes y los múltiples elementos relacionados con el transporte de petróleos pesados por sistemas de tuberías.

La comprensión de la reología del combustible crudo tiene gran uso práctico en relación con sus parámetros de flujo al transportarlos a través de las tuberías. El interés por el tema va acentuado debido a la creciente utilización de petróleos crudos de alta viscosidad en centrales termoeléctricas y plantas metalúrgicas. La obtención de los resultados implica modelos experimentales, además de la obtención de un modelo específico en la interpretación del efecto de la temperatura y el gradiente de velocidad sobre la viscosidad del combustible pesado.

El laboratorio de Mecánica de los Fluidos de la Universidad de Moa cuenta con equipos y medios tecnológicos en una instalación que puede ser adaptado para el transporte del crudo pesado cubano. En este trabajo se propone el rediseño a escala experimental de la instalación de hidrotransporte del laboratorio de hidráulica de la Universidad de Moa para el manejo del Crudo Mejorado 650.

Materiales y métodos

A partir del estudio reológico realizado por Laurencio (2012), se obtuvieron los resultados que muestra la Figura 1, en la misma se recoge la dependencia entre el esfuerzo de corte y el gradiente de velocidad para las temperaturas experimentadas. Al representar gráficamente los datos experimentales de t en función del g  se trazaron las curvas de flujo que permiten realizar el ajuste de los datos obtenidos.

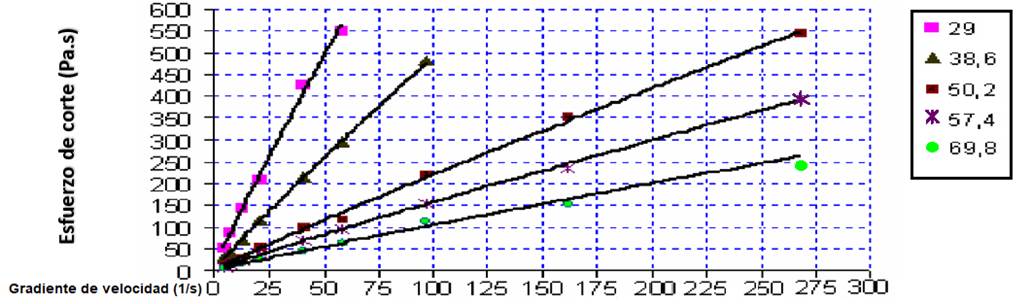
Figura 1. Curvas de flujo del combustible cubano CM-650 en función de la temperatura (Laurencio, 2012).

El combustible cubano CM-650 mostró el mejor ajuste para el modelo de fluido seudoplásticos, corroborándose lo planteado por Laurencio (2012). El comportamiento manifestado, está caracterizado por los parámetros reológicos, índice de consistencia másica (K) e índice de flujo (n). En cuanto a los parámetros reológicos, se identificó la tendencia respecto a la dependencia de cada factor con la temperatura. Los modelos ajustados para cada temperatura se exponen en la Tabla 1 (Laurencio, 2012).

Tabla 1. Correlaciones de esfuerzo de corte en función del gradiente de velocidad

Temperatura	Modelo ajustado
29 °C
38,6 °C
50,2 °C
57,4 °C
69,8 °C

A través de las correlaciones de esfuerzo de corte para las diferentes temperaturas analizadas se determinan los parámetros reológicos y los coeficientes obtenidos del ajuste del modelo reológico realizado por Laurencio (2012) (Tabla 2).

Tabla 2. Parámetros reológicos y coeficiente de correlación múltiple

N°	Parámetros	Temperatura
		29 °C	38,6 °C	50,2 °C	57,4 °C	69,8 °C
1	K (Pa.s)	13,55	6,89	3,097	2,22	1,46
2	n (adim.)	0,917	0,926	0,926	0,925	0,929
3	R2	0,997	0,999	0,997	0,998	0,997

El coeficiente de correlación múltiple (R²) en todos los casos fue superior a 0,996; por lo que se considera satisfactorio el ajuste de los modelos a los datos experimentales, indicativo de que se experimenta un fluido estable.

Descripción de la instalación a escala experimental del laboratorio de Hidráulica de la Universidad de Moa

La instalación se diseñó para realizar pruebas hidráulicas con fluidos viscosos a temperatura ambiente, en esta investigación se propone rediseñar la instalación para la evaluación de los combustibles cubanos pesados.

La instalación está compuesta por una tubería de 25,4 mm de diámetro nominal; 26,64 mm de diámetro interior y 33,4 mm de diámetro exterior; con una extensión de tubería recta de 8,27 m. En la cual se utilizan manómetros en un tramo de tubería horizontal a una distancia de 2,5 m, a 60 veces el diámetro de la tubería a la entrada y 40 a la salida como se muestra en la figura 2; las cuales constituyen las dimensiones recomendadas para reducir los errores en las mediciones (Casals 2015; Williams 2016; Reza 2000).

;

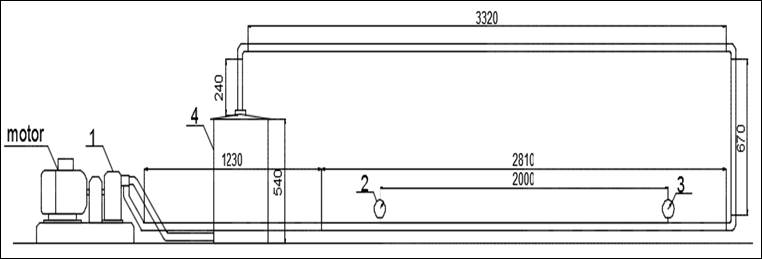
Figura 2. Esquema de la instalación de hidrotransporte a escala experimental.

Evaluación del sistema de bombeo para el transporte del crudo cubano mejorado CM-650 en la instalación experimental de la Universidad de Moa

Teniendo en cuenta un caudal controlado de 57 l/min equivalente a 0,00095 m³/s, se estableció una metodología de evaluación del sistema de bombeo propuesta por (Hinojosa, 2019), donde por la naturaleza reológica del fluido el número de Reynolds se puede establecer según Laurencio (2012).

Donde:

K: Índice de consistencia, (Pas)

r: Densidad del fluido, (kg/m³)

n: Índice de flujo, (adimensional).

Para determinar la densidad se apoyó de la investigación realizada por Laurencio (2012):

r = [-7.62·In (T) + 1012]

Donde:

T: Temperatura del fluido, (⁰C)

Cálculo de las pérdidas por rozamiento

Para el cálculo de las perdidas por rozamiento se utilizan las expresiones matemáticas propuestas por la literatura técnica (Garcell el al., 2011; Laurencio, 2012) y las pérdidas en la succión y en la impulsión respectivamente, por la expresión de Nekrasov (1968).

En la tabla 4, se muestran los accesorios de la instalación de bombeo experimental.

Tabla 3. Accesorios en la succión y descarga de la instalación

Accesorios DN ½ pul.	cantidad	accesorios	cantidad
Entrada al tanque	1	Salida de tubería	1
Ensanchamiento	1	Codo de 90°	3
Codo de 45°	2	-	-

Cálculo del espesor del aislamiento térmico para las tuberías de acero al carbono

Para el análisis del espesor de aislamiento térmico en las tuberías de la instalación experimental para el transporte del Crudo Cubano Mejorado 650, se realizó considerando un espesor de aislamiento térmico recomendado para el diámetro nominal de la tubería y se seleccionó como material aislante lana de vidrio, como se muestra en la tabla 4.

Tabla 4. Espesores recomendados para aislamiento térmico Ta= 25 °C (77 °F)

Temperatura de operación		Hasta 65 °C (150 °F)
		E.S.		P.C.		T.S.
DN del Tubo
Pulg.	mm	Pulg.	mm	BTU/h.ft	W/m	°C	°F
1/2	12,7	1	25,4	7,44	7,15	28,7	83,6
3/4	19,1	1	25,4	8,95	8,60	29,4	84,9
1	25,4	1	25,4	9,28	8,92	28,8	83,9

Para ver el comportamiento y la evaluación de la selección del espesor y tipo de aislamiento térmico se parte de la idea de calcular las pérdidas de calor en las tuberías sin aislamientos térmico y con aislamientos térmicos, pudiendo ver el porciento de reducción de las pérdidas de calor cuando se utiliza aislamiento térmico con respecto a una tubería sin insulación. Es importante considerar que las pérdidas de calor se determinaron por cada un metro de longitud de tubería, considerando una temperatura operacional del fluido a 70 ⁰C.

Cálculo de las pérdidas de calor por conducción y convección para una tubería sin aislamiento térmico

La figura 3 muestra un tramo de tubería sin aislamiento térmico en este caso se calcularon las pérdidas de calor para los diámetros nominales de tuberías de media pulgada y una pulgada (Garcell et al. 2011).

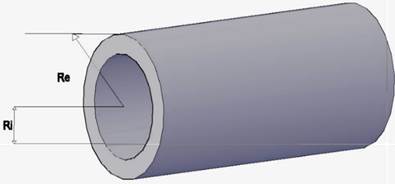
Figura 3. Tubería sin aislamiento térmico.

Como se muestra en la figura 3 el fluido caliente circula por dentro de la tubería y por fuera de la tubería circula el aire a la temperatura exterior del medio ambiente.

Para la determinación del coeficiente de convección del fluido interior se emplea la ecuación propuesta por Laurencio (2012).

Donde:

R_e: Número de Reynolds para el combustible CM 650, (adimensional)

P_r: Número de Prandt, (adimensional)

D_i: Diámetro interior de la tubería, (m)

k_p: Coeficiente de conductividad térmica del petróleo y del aire, (W/m·^oC)

Los valores del Prandt y del coeficiente de conductividad térmica del petróleo crudo cubano mejorado 650 según Laurencio (2012) se determinan por las ecuaciones:

Para determinar el coeficiente de convección del aire es necesario determinar el número de Reynolds del aire en exterior de la tubería:

Donde:

m_a: Viscosidad plástica del aire, (Pas)

r: Densidad del aire, (kg/m³)

u_a: Velocidad del aire (se asume 8 m/s para sistemas con circulación de aire)

El área de transferencia aumenta con la distancia entre r₀ y r₁. El calor fluye hacia fuera del cilindro, ya que se ha supuesto que T_i >T_e (temperatura interior y exterior respectivamente). Por lo que se puede plantear la metodología a emplear según la modelación matemática expuesta por Garcell, Díaz & Surís (2011), donde el coeficiente global de transferencia de calor para dicha tubería se determina por la ecuación:

La expresión para el flujo de calor total será descrita por la ecuación:

Q= U_w ·A_c ·DT_m

Donde:

A_c: Área de la circunferencia exterior, (m²)

Q: Pérdida de calor total en la tubería por cada un metro de longitud de tubería, (W/m).

Cálculo de las pérdidas de calor por conducción y convección para una tubería con aislamiento térmico

En la figura 4, se muestra un tramo de tubería con aislamiento térmico en este caso se calcularon las pérdidas de calor para los diámetros nominales de tuberías de media pulgada y una pulgada igualmente que en el caso anterior (Garcell et al. 2011).

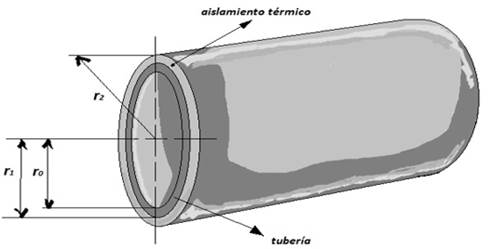
Figura 4. Tubería con aislamiento térmico.

Como se muestra en la figura 4 el fluido caliente (Crudo Mejorado 650) circula por dentro de la tubería y por fuera del conducto circula el aire a la temperatura exterior del medio ambiente, importante señalar que el sistema está compuesto por dos capas, la primera capa es la tubería de acero al carbono y la segunda capa es del material aislante, en este caso es lana de vidrio.

En la figura anterior se observa que el área de transferencia aumenta con la distancia entre r₀ y r₂. En este caso el calor fluye hacia fuera del cilindro, ya que se ha supuesto que T_i >T_e (temperatura interior y exterior respectivamente).

Aplicando la metodología de perdida de calor de una tubería sin aislamiento, y añadiendo una tercera capa que es la insulación de la tubería, se obtiene la ecuación para el flujo total de calor.

Q = U · Ac (DT_m)

Donde:

A_c: área de la circunferencia de radio 2 (m²)

La variación de temperatura entre la capa interior y la exterior se determina a partir de la diferencia media logarítmica, en función de la temperatura que entra y sale del tanque. Esta variación de temperatura se describe en la figura 5, reflejándose las pérdidas de temperatura del sistema, de alrededor de 5 ⁰C.

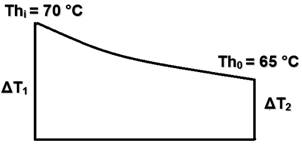
Figura 5. Variación de temperatura en la cual sale y entra el fluido en el tanque.

La diferencia media logarítmica se determina por la ecuación:

Donde:

DT_ml: Diferencia media logarítmica, ^oC

DT₁: Variación de temperatura inicial del fluido en el tanque (a la salida del tanque), ^oC

DT₂: Variación de temperatura final del fluido en el tanque (a la entrada del tanque), ^oC

DT₁ = T_hi - T_a

Donde:

T_a: 250 ^oC Temperatura ambiente del aire

T_hi: Temperatura del fluido a la salida del tanque, ^oC

DT₂ = T_h0 - T_a

Donde:

Th₀: Temperatura del fluido a la entrada al tanque, ⁰C

Cálculo de las pérdidas de calor por conducción y convección para el tanque, con aislamiento y sin aislamiento térmico

En el caso del tanque se determinan las pérdidas de energía o de calor sin aislamiento térmico y con aislamiento térmico igualmente que, en el sistema de tuberías y accesorios, por el mismo procedimiento descrito anteriormente, considerando el tanque como si fuera un conducto cilíndrico. En este caso cambia la geometría del sistema siendo el tanque de mayor diámetro.

Resultados y discusión

Evaluación del sistema de bombeo para el manejo del crudo mejorado CM-650 en la instalación semi-industrial de la Universidad de Moa

En la evaluación del sistema de bombeo perteneciente al laboratorio de hidráulica de la Universidad de Moa se emplea una bomba de desplazamiento positivo de engranaje donde el fluido circula por el diámetro interior de 0,0158 m para la tubería de DN (diámetro nominal) 12,7 mm. El fluido en estudio se analizó para una temperatura de operacional de 70 °C. En la tabla 5 se muestran los valores obtenidos de la evaluación del sistema de bombeo.

Tabla 5. Resultado de los cálculos para los tramos de media y una pulgada respectivamente

Tubería de DN (1/2 pul) (12,7 mm)	Valor obtenido	Tubería de DN (1 pul) (25,4 mm)	Valor obtenido
Resultados de las v (m/s)	4,845	Resultados de las v (m/s)	0,000195
Resultados de las Áreas (m2)	0,987	Resultados de las Áreas (m^2)	0,000961
Número de Reynolds Re	87,8	Número de Reynolds Re	33,5
Factor de fricción	0,73	Factor de fricción	1,91
Pérdida por rozamiento en la tubería de succión (h1) m	45,52	Pérdida por rozamiento en la tubería de descarga (h1) m	51,65
Pérdida local en la tubería de succión de DN 12,7 mm (h2) m	3,84	Pérdida local en la tubería de descarga (h2) m	0,46
Sumatoria del coeficiente de pérdida local en la tubería de succión (ξt)	3,21	Sumatoria del coeficiente de pérdida local en la tubería de descarga (ξt)	3,07
Pérdidas totales en la tubería de succión (ht) m	49,36	Pérdidas totales en la tubería de impulsión (himp) m	52,1
Pérdida por rozamiento en la tubería de descarga (h1) m	70,1	Pérdidas totales en la tubería de impulsión (himp) m	91,27
Pérdida local en la tubería de descarga (h2) m	2,26	Pérdidas dinámicas (hdin) m	140,6
Sumatoria del coeficiente de pérdida local en la tubería de descarga (ξt)	1,891	Altura estática () m	0,435
Pérdidas totales en la tubería de impulsión (himp) m	72,33	Pérdidas totales en el sistema (ht) m	141,1

Teniendo en cuenta los resultados obtenidos las pérdidas totales son de 141,1 m de columna líquida. Este valor se encuentra por debajo de la presión máxima por diseño de la bomba facilitada por el fabricante de 20,6 MPa que esto equivale a una presión de 2100,6 m de columna líquida superior a la calculada. Por lo que se puede plantear que la bomba se puede utilizar para transportar el fluido en estudio en la instalación.

Resultados de los cálculos del espesor del aislamiento térmico para las tuberías de acero al carbono

El aislamiento térmico utilizado en la instalación es la lana de vidrio con coeficiente de conductividad térmica de 0,034 W/m^oC. El espesor de aislamiento térmico utilizado es de 25,4 mm (1 pul), se calcularon las pérdidas de energía para la tubería sin aislamiento térmico y con aislamiento térmico, donde se pudo comprobar el porciento de reducción de las mismas y ver la factibilidad de utilizar el aislamiento térmico en el sistema para garantizar la menor pérdida de energía.

Resultados del cálculo de las pérdidas de calor por conducción y convección para una tubería sin aislamiento térmico y con aislamiento térmico

En las tablas 6 y 7 se recogen los resultados obtenidos de los coeficientes por transferencia de calor por conducción y convección del Crudo Cubano 650 y del aire y el cálculo de las pérdidas de calor de la instalación hidráulica a escala experimental, para los tramos de tubería de media y una pulgada con y sin aislamiento térmico respectivamente, estableciendo una comparación de los valores obtenidos. Se observa el comportamiento de las pérdidas de calor del fluido hacia el exterior.

Tabla 6. Resultados del cálculo de las pérdidas de calor sin aislamiento térmico para los tramos de tubería de media y una pulgada

Coeficientes por transferencia de calor para el tramo de media pulgada (12,7 mm)	Valor obtenido	Coeficientes por transferencia de calor para el tramo de una pulgada (25,4 mm)	Valor obtenido
Prandt (Pr)	7278,5	Prandt (Pr)	8183,4
Coeficiente de transferencia de calor por conducción del acero al carbono (kA)W/m· ºC	60,5	Coeficiente de transferencia de calor por conducción del acero al carbono (kA) W/m· ºC	60,5
Coeficiente de conductividad térmica del petróleo (kp)W/m·ºC	0,14	Coeficiente de conductividad térmica del petróleo (kp)W/m·ºC	0,14
Coeficiente de transferencia de calor por convección del combustible CM 650 (hi)W/m·0C	105,3	Coeficiente de transferencia de calor por convección del combustible CM 650 (hi)W/m·oC	39,1
Coeficiente de transferencia de calor por convección del aire (he)W/m ºC	79,2	Coeficiente de transferencia de calor por convección del aire (he)W/m·oC	66,2
Número de Reynolds para el aire (Re)	10720,615	Número de Reynolds para el aire (Re)	16 810,73
Coeficiente de conductividad térmica del aire (kp) W/m·ºC	26,3·10-3	Coeficiente de conductividad térmica del aire (kp) W/m·ºC	26,3·10-3
Coeficiente global de transferencia de calor (Uw) W/m2·ºC	45,1	Coeficiente global de transferencia de calor (Uw) W/m2·ºC	24,6
Área de la circunferencia (Ac) m2	0,067	Área de la circunferencia (Ac) m2	0,105
Pérdida de calor total en la tubería por cada un metro de longitud de tubería (Q) W/m	122,1	Pérdida de calor total en la tubería por cada un metro de longitud de tubería (Q) W/m	104,2

Se determinaron las pérdidas totales de energía al exterior por cada un metro de longitud de tubería recta para media pulgada y una pulgada dando un valor de 122,1 W/m y 104,2 W/m respectivamente sin aislamiento térmico, siendo valores relativamente alto.

La tabla 7 muestra los resultados obtenidos cuando la tubería tiene insulación. Se puede observar el comportamiento de los valores obtenidos y las pérdidas de calor.

Tabla 7. Resultados del cálculo de las pérdidas de calor con aislamiento térmico para los tramos de tubería de media y una pulgada

Coeficientes por transferencia de calor para el tramo de media pulgada    (12,7 mm)	Valor obtenido	Coeficientes por transferencia de calor para el tramo de una pulgada (25,4 mm)	Valor obtenido
Coeficiente de transferencia de calor por convección del aire (he)W/m·0C	48,6	Coeficiente de transferencia de calor por convección del aire (he)W/m·oC	45,7
Número de Reynolds para el aire (Re)	36289,031	Número de Reynolds para el aire (Re)	42397,146
Coeficiente global de transferencia de calor (Uw)W/m2·ºC	0,7	Coeficiente global de transferencia de calor (Uw)W/m2·ºC	0,8
Área de la circunferencia (Ac)m^2	0,227	Área de la circunferencia (Ac)m^2	0,265
Pérdida de calor total en la tubería por cada un metro de longitud de tubería(Q) W/m	6,8	Pérdida de calor total en la tubería por cada un metro de longitud de tubería (Q)W/m	9

Teniendo en cuenta los valores analizados las pérdidas totales sin aislamiento térmico y con aislamiento térmico, se pudo demostrar que para una tubería de diámetro nominal de media pulgada los porcientos de reducción de las pérdidas de calor están en orden de 94,4 %. Así como para una tubería de diámetro nominal de una pulgada los porcientos de reducción de las pérdidas de calor están en el orden de 91 %, siendo factible utilizar aislamiento térmico en la tubería con un espesor de 25,4 mm (1 pulgada).

Resultados del cálculo de las pérdidas de calor por conducción y convección para el tanque con aislamiento térmico y sin aislamiento térmico

Considerando el tanque de la instalación como un conducto se determinaron las pérdidas de energía con aislamiento térmico y sin aislamiento térmico. Las pérdidas de calor se calcularon en las paredes del tanque utilizando la geometría del mismo, para un diámetro exterior del tanque de 0,380 m, un espesor de 8 mm y una altura de 0,540 m.

En la tabla 8 se muestran los valores obtenidos del cálculo de las pérdidas por conducción y convección para el tanque estableciendo una comparación.

Tabla 8. Resultados del cálculo de los coeficientes por transferencia de calor por conducción y convección del aire y el Crudo Mejorado 650

Sin aislamiento térmico	Valor obtenido	Con aislamiento térmico	Valor obtenido
Prandt (Pr)	14743,2	-	-
Coeficiente de transferencia de calor por convección del combustible CM 650 (hi)W/m·^0C	0,3	-	-
Coeficiente de transferencia de calor por convección del aire (he)W/m·^0C	25	-	-
Número de Reynolds para el combustible CM 650 (Re)	1,955	-	-
Número de Reynolds para el aire (Re)	191259,805	-	-
Coeficiente global de transferencia de calor (Uw)W/m^2·ºC	0,3	Coeficiente global de transferencia de calor (Uw)W/m^2·ºC	0,2
Área de la circunferencia (Ac)m^2	0,645	Área de la circunferencia (Ac)m^2	0,143
Pérdida de calor total en la tubería por cada un metro de longitud de tubería (Q)W/m^2	6,9	Pérdida de calor total en la tubería por cada un metro de longitud de tubería (Q)W/m^2	1,2

Con el análisis realizado se pudo observar que las pérdidas totales de energía al exterior para el tanque sin aislamiento térmico se obtiene un resultado de 6,9 W/m², mientras que para el tanque con aislamiento térmico se obtiene un valor relativamente pequeño por lo que se pudo demostrar que utilizando aislamiento térmico en las paredes del tanque se puede reducir las pérdidas en energía en el orden de 83,3 %, siendo factible.

Selección del calentador del tanque

La selección del calentador del tanque se fundamenta en lo planteado anteriormente, importante resaltar que se utilizará un calentado por resistencia eléctrica de la firma Polimex (Productos de Calefacción Industrial), de la figura 6, se selecciona el calentador por resistencia eléctrica de material de cobre con una temperatura máxima de operación de 180 ⁰C, y un consumo de potencia de 65 W/pul que esto equivale a 10 W/cm.

Conclusiones

A través de la caracterización reológica del fluido en estudio el Crudo Cubano Mejorado 650 permitió una evaluación real del sistema de bombeo a escala experimental del laboratorio de hidráulica, con una presión de descarga consumida de 141,1 m de columna líquida, por debajo de la de diseño propuesta por el fabricante.

Con la propuesta del espesor de aislamiento térmico de una pulgada (25,4 mm), se podrían reducir las pérdidas de energía en el orden del 89,56 % en la instalación de bombeo experimental.

Se puede proponer el calentador del tanque en la instalación experimental, utilizando resistencia eléctrica de la firma Polimex, para una temperatura máxima de trabajo de 180 ⁰C, y un consumo de potencia de 10 W/cm.

Referencias bibliográficas

Casals, J. (2015). Procedimiento para prácticas de laboratorio en la asignatura Mecánica de los Fluidos. (Trabajo de diploma, Instituto Superior Minero Metalúrgico de Moa). http://ninive.ismm.edu.cu/handle/123456789/2547

Garcell, L.; Díaz, A. &  Surís, G. (2011). Transferencia de cantidad de movimiento, color y masa. Félix Varela.

Hinojosa  J. (2019). Cálculo verificativo del bombeo de desechos lixiviados (cola) hacia el nuevo depósito. (Trabajo de diploma, Universidad de Moa). http://ninive.ismm.edu.cu/handle/123456789/3710

Laurencio, H. (2012). Método para la determinación de parámetros racionales de transporte por tuberías del combustible cubano crudo mejorado 650. (Tesis doctoral, Instituto Superior Minero Metalúrgico). http://ninive.ismm.edu.cu/handle/123456789/1540

Laurencio, H., Falcón, J., Retirado, Y. & Pérez, O. (2012). Modelo para cálculo de pérdidas de presión en tuberías conductoras de petróleo pesado (11º API). Minería y Geología 28(3), 70-86. https://revista.ismm.edu.cu/index.php/revistamg/article/view/310

Laurencio, H., Retirado, Y., Falcón, J., Torres, E. & Salazar, M. (2022). Modelo para simulación de la potencia de flujo en tuberías conductoras de petróleo pesado con comportamiento seudoplástico. Ingeniare. Revista chilena de ingeniería, 30(1), 171-179. https://revistas.uta.cl/pdf/2879/0718-3305-ingeniare-30-01-171.pdf

Laurencio, H. y Delgado, Y. (2008). Propiedades reológicas de emulsiones de petróleo pesado en agua. Ingeniare. Revista chilena de ingeniería, 16(1), 244-249. https://revistas.uta.cl/pdf/1540/art14.pdf

Nekrasov, B. (1986). Hidraúlica. Editorial Pueblo Y Educación, La Habana.

Reza, G. (2000). Flujo de fluidos en válvulas, accesorios y tuberías. McGraw-Hill.

Williams, M. (2016). Determinación de la velocidad crítica en el transporte de la pulpa laterítica en la fábrica "Pedro Sotto Alba". (Trabajo de diploma, Universidad de Moa). http://ninive.ismm.edu.cu/handle/123456789/2526